Introduction
Overview
Teaching: 20 min
Exercises: 0 minQuestions
How shared memory parallel programs work?
What is OpenMP?
How to write and compile parallel programs in C?
Objectives
Understand the shared memory programming environment provided by OpenMP
Learn how to write and compile simple parallel programs in C
Shared Memory OpenMP Programming Overview
- The OpenMP standard outlines how parallel programs should be written for shared memory systems.
- The majority of compilers support OpenMP.
View OpenMP specifications
View Full List of Compilers supporting OpenMP
For an overview of the past, present and future of the OpenMP read the paper “The Ongoing Evolution of OpenMP”.
OpenMP Execution Model
-
OpenMP programs realize parallelism through the use of threads.
-
Parallel OpenMP execution is based on a concept called fork-join:
- An OpenMP program starts as a single thread, the master thread.
- The master thread creates a team of parallel threads.
- Team threads execute statements in parallel.
- Team threads synchronize and terminate.
- Memory is categorized into two types: shared and thread-local.
Compiling OpenMP Programs
Create a working directory in ~/scratch:
cd ~/scratch
Code examples on the training cluster can be obtained by following these steps:
cp /tmp/omp_workshop_2024.tar .
tar -xf omp_workshop_2024.tar
If you are using a real cluster, you can download examples from the web:
wget https://github.com/acenet-arc/ACENET_Summer_School_OpenMP_ACC/raw/gh-pages/code/omp_workshop_2024.tar
tar -xf omp_workshop_2024.tar
A Very Quick Introduction to C
Preprocessor Directives
- The
#includedirective inserts the contents of a file.
#include <header_file.h>
- The
#definedirective declares constant values.
# define SIZE 1000
- The conditional group
#ifdef.
#ifdef MACRO
controlled code
#endif
Basic Syntax
{ ... }Curly braces are used to group statements into blocks.;The semicolon operator is used to separate statements-
,The comma operator separates expressions (which have value) - For Loop
for ([initialization]; [condition test]; [increment or decrement]) { //Statements to be executed repeatedly } - Example for loop:
int i,c; for(i=10,c=1;i<100;i++) { c += 2*i; } - Any statements in a for loop can be skipped, but semicolons must remain. For example, you can do initialization before loop:
i=10, c=1; for(; i<100; i++) { c += 2*i; } - Skipping all loop statements will result in an infinite loop:
for(;;)
Functions
- The format of function definitions is as follows:
return_type function_name( parameters ) { body } - Here is an example of a function that finds the maximum of two numbers:
int max(int num1, int num2) { int result; if (num1 > num2) result = num1; else result = num2; return result; }
Pointers
-
Pointers are special variables used to store addresses of variables rather than values.
-
The
&operator (reference) returns the variable’s address: address of A is&A.
- The
*symbol has two meanings- The
*operator (dereference) allows you to access an object through a pointer.*X, for example, will give you the value of variableXifXis the memory address where it is stored. - In the statement
float* my_array;the variablemy_array;is defined as a pointer to a location in memory containing floating-point numbers.
- The
Arrays
- Static arrays.
int A[500];
- Dynamic arrays.
int * A;
size = 500; // Define array size
A = (int *)malloc(size*sizeof(int)); // Allocate memory
A = (int *)realloc(A,1000); // Increase size
A[i]=10; // Set array elements
free(A); // Free memory
Compiling C Code
Using C compilers on Compute Canada Systems
- Currently the default environment on all general purpose clusters (Beluga, Cedar, Graham, Narval) is
StdEnv/2023.- The default compilers available in this environment on Graham and Beluga are
intel/2023.2.1andgcc/12.3.- To load another compiler you can use the command
module load. For example, the command to loadgcc/10.3.0is:module load StdEnv/2020 gcc/10.3.0
Training cluster
The default environment on the training cluster is StdEnv/2020. We will use gcc/9.3.0
module load StdEnv/2020 gcc/9.3.0
- Intel compilers are not available on the traiining cluster
The following is an example of a simple hello world program written in C.
/* --- File hello_serial.c --- */
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char **argv) {
printf("Hello World\n");
}
In order to compile this code, you would need to use the following command:
gcc -o hello hello_serial.c
This gives you an executable file hello that will print out the text “Hello World”. You run it with the command:
./hello
Hello World
- If you don’t specify the output filename with the
-ooption compiler will use the default output name a.out (assembler output).
Key Points
Shared-memory parallel programs break up large problems into a number of smaller ones and execute them simultaneously
OpenMP programs are limited to a single physical machine
OpenMP libraries are built into all commonly used C, C++, or Fortran compilers
A Parallel Hello World Program
Overview
Teaching: 20 min
Exercises: 10 minQuestions
How do you compile and run an OpenMP program?
What are OpenMP pragmas?
How to identify threads?
Objectives
Write, compile and run a multi-threaded program where each thread prints “hello world”.
Adding Parallelism to a Program
OpenMP core syntax
#pragma omp <directive> [clause] ... [clause]
- All OpenMP pragmas begin with
#pragma omp - Directive specifies the parallel action
- Optional clause[s] describe additional behavior
How to add parallelism to the basic hello_world program?
- Include OpenMP header
- Use the
paralleldirective
Begin with the file hello_template.c.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char **argv) {
printf("Hello World\n");
}
Make a copy named hello_omp.c.
- To make hello_omp.c parallel, add the following code:
...
#include <omp.h>
...
int main(int argc, char **argv) {
#pragma omp parallel
...
}
hello_omp.c
How to compile an OpenMP program?
- Compiling OpenMP code requires the use of a compiler flag (
-fopenmpfor GCC,-qopenmpfor Intel).
gcc -fopenmp -o hello hello_omp.c
icc -qopenmp -o hello hello_omp.c
Running an OpenMP program
- Use the environment variable
OMP_NUM_THREADSto control the number of threads.
export OMP_NUM_THREADS=3
./hello
How does the parallel hello_world program work?
- The compiler generates code that starts a number of threads equal to the number of available cores or to the value of the variable OMP_NUM_THREADS (if it is set).
- Each team thread then executes the function
printf("Hello World\n") - Threads rejoin the main thread when they return from the
printf()function. At this point, team threads are terminated and only the main thread remains. - After reaching the end of the program, the main thread terminates.
Using multiple cores
Try running the
helloprogram with different number of threads.
- Is it possible to use more threads than the number of cores on the machine?
You can use the
nproccommand to find out how many cores are on the machine.Solution
Since threads are a programming abstraction, there is no direct relationship between them and cores. In theory, you can launch as many threads as you like. However, if you use more threads than physical cores, performance may suffer. There is also a possibility that the OS and/or OpenMP implementation can limit the number of threads.
OpenMP with SLURM
To submit an OpenMP job to the SLURM scheduler, you can use the following submission script template:
#!/bin/bash #SBATCH --cpus-per-task=4 ./helloSubmission scripts are submitted to the queue with the
sbatchcommand:sbatch <submission_script>You can also ask for an interactive session with multiple cores like so:
[user45@login1 ~]$ salloc --mem-per-cpu=1000 --cpus-per-task=2 --time=1:0:0salloc: Granted job allocation 179 salloc: Waiting for resource configuration salloc: Nodes node1 are ready for job [user45@node1 ~]$The most practical way to run our short parallel program on our test cluster is using the
sruncommand. It will run the program on the cluster from the interactive shell.
- All three commands (
sbatch,sallocandsrun) accept the same keywords.srun --cpus-per-task=4 hello # or even shorter: srun -c4 hello
Identifying threads
How can we tell which thread is doing what?
- The function
omp_get_thread_num()returns the thread ID of the currently running process.
...
#pragma omp parallel
{
int id = omp_get_thread_num();
printf("Hello World from thread %d\n", id);
}
...
- Another useful function is
omp_get_num_threads(), which returns the number of threads.
Thread ordering
Run the
helloprogram several times.
In what order do the threads write out their messages?
What is happening here?Solution
The messages are emitted in random order. This is an important rule of not only OpenMP programming, but parallel programming in general: parallel elements are scheduled to run by the operating system and order of their execution is not guaranteed.
Conditional Compilation
We said earlier that you should be able to use the same code for both OpenMP and serial compillation. Try compiling the code without the
-fopenmpflag.
- What happens?
- Can you figure out how to fix it?
Hint: The -fopenmp option defines preprocessor macro
_OPENMP. The#ifdef _OPENMPpreprocessor directive can be used to tell the compiler to process the line containing the omp_get_thread_num( ) function only if the macro exists.Solution
... #ifdef _OPENMP printf("Hello World %i\n", omp_get_thread_num()); #else printf("Hello World \n"); #endif ...hello_omp.c
OpenMP Constructs
- Directives combined with code form a construct:
#pragma omp parallel private(thread_id) shared(nthreads)
{
nthreads = omp_get_num_threads();
thread_id) = omp_get_thread_num();
printf("This thread %d of %d is first\n", id, size);
}
Parallel Construct
- In general parallel consruct, it’s up to you to decide what work each thread takes on.
The omp single
- By using a single directive, we can run a block of code by just one thread, the thread that encounters it first.
View more information about the omp single directive
Which thread runs first?
Modify the following code to print out only the thread that gets to run first in the parallel section. You should be able to do it by adding only one line. Here’s a (rather dense) reference guide in which you can look for ideas: Directives and Constructs for C/C++.
#include <stdio.h> #include <stdlib.h> #include <omp.h> int main(int argc, char **argv) { int id, size; #pragma omp parallel private(id,size) { size = omp_get_num_threads(); id = omp_get_thread_num(); printf("This thread %d of %d is first\n", id, size); } }Solution
... id = omp_get_thread_num(); #pragma omp single ...first_thread.c
Key Points
OpenMP pragmas direct the compiler what to parallelize and how to parallelize it.
By using the environment variable
OMP_NUM_THREADS, it is possible to control how many threads are used.The order in which parallel elements are executed cannot be guaranteed.
A compiler that isn’t aware of OpenMP pragmas will compile a single-threaded program.
OpenMP Work Sharing Constructs
Overview
Teaching: 20 min
Exercises: 10 minQuestions
During parallel code execution, how is the work distributed between threads?
Objectives
Learn about the OpenMP constructs for worksharing.
- OpenMP offers several types of work sharing constructs that assist in parallelization.
- The work-sharing constructs do not create new threads, instead they use a team of threads created by the
paralleldirective. - At the end of a work-sharing construct, a program will wait for all threads to complete. This behavior is called an implied barrier.
The omp parallel for
- divides loop iterations across threads.
- used after a parallel region has been created.
- each thread executes the same instructions (data parallelism).
...
#pragma omp parallel for
for (i=0; i < N; i++)
c[i] = a[i] + b[i];
...
The omp sections
- used to divide the work into distinct, discrete parts.
- specify that the enclosed sections of code should be divided among threads.
- employed in non-iterative work-sharing constructs.
- more than one section can be executed by a thread.
Functional parallelism can be implemented using sections.
...
#pragma omp parallel shared(a,b,c,d) private(i)
{
#pragma omp sections nowait
{
#pragma omp section
for (i=0; i < N; i++)
c[i] = a[i] + b[i];
#pragma omp section
for (i=0; i < N; i++)
d[i] = a[i] * b[i];
} /* end of sections */
} /* end of parallel region */
...
nowait - do not wait for all threads to finish.
Using parallel sections with different thread counts
Compile the file sections.c and run it with a different number of threads. Start with 1 thread:
srun -c1 ./a.outIn this example there are two sections, and the program prints out which thread is handling which section.
- What happens if the number of threads and the number of sections are different?
- More threads than sections?
- Less threads than sections?
Solution
If there are more threads than sections, only some threads will execute a section. If there are more sections than threads, the implementation defines how the extra sections are executed.
Applying the parallel directive
What will the following code do?
omp_set_num_threads(8); #pragma omp parallel for(i=0; i < N; i++){C[i] = A[i] + B[i];}Answers:
- One thread will execute each iteration sequentially
- The iterations will be evenly distributed across 8 threads
- Each of the 8 threads will execute all iterations sequentially overwriting the values of C.
Solution
The correct answer is 3.
Key Points
Data parallelism refers to the execution of the same task simultaneously on multiple computing cores.
Functional parallelism refers to the concurrent execution of different tasks on multiple computing cores.
Parallel Operations with Arrays
Overview
Teaching: 20 min
Exercises: 20 minQuestions
How do I parallelize a loop?
How do I ensure that the parallel code gives correct results?
Objectives
Learn to use the
parallel forpragmaLearn to use the
privateclauseBe able to identify data dependencies
- A single CPU cannot efficiently handle array operations
- Large-scale linear algebra problems can be efficiently solved with OpenMP
C arrays - static and dynamic
Declaring static arrays:
A[2048][2048];Disadvantages:
- Allocated when a program starts
- Occupies memory until a program ends.
- Allocated on the stack. There may be a limit on the stack allocation
- The stack memory limit can be checked with the command:
ulimit -s
- If you want to modify the stack memory limit, you can use the ulimit command:
ulimit -s unlimited
- On compute nodes stack is unlimited
Testing static and dynamic memory allocation with a simple program:
/* --- File test_stack.c --- */ #include <stdio.h> #include <stdlib.h> #define N_BYTES 10000000 // 10 MB void test_heap(int N) { char *B; B=malloc(N*sizeof(char)); // Allocating on heap printf("Allocation of %i bytes on heap succeeded\n", N); free(B); } void test_stack(int N) { char A[N]; // Allocating on stack printf("Allocation of %i on stack succeeded\n", N); } int main(int argc, char **argv) { test_heap(N_BYTES); test_stack(N_BYTES); }
Multiplying an Array by a Constant
- Serial code loops over all array elements as follows:
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
int main(int argc, char **argv)
{
double start, end;
int size = 5e8;
int multiplier = 2;
int *A, *C;
int i;
/* Allocate memory for arrays */
A = malloc(size * sizeof(int));
C = malloc(size * sizeof(int));
start = omp_get_wtime();
/* Multiply array a by multiplier */
for (i = 0; i < size; i++)
{
C[i] = multiplier * A[i];
}
end = omp_get_wtime();
printf("Total time is %f s\n", end-start);
}
- The omp_get_wtime( ) function is used to determine the start and end times for the loop.
Compiling and Running a Serial Version
Compile the program.
gcc array_multiply_serial.c -o array_multiply_serial -fopenmp
Run it on the cluster.
srun --mem=5000 array_multiply_serial
Execution time and array size
Run the program several times and observe execution time.
- How does the program perform over multiple runs?
Change the size of the array, recompile and rerun the program. Record execution time.
- How did the size of the array affect execution time?
Creating a Parallel Version
- We need to tell compiler that we want to parallelize the main
forloop.
...
/* Multiply array a by multiplier */
#pragma omp parallel for /* <--- OpenMP parallel for loop --- */
for (i = 0; i < size; i++)
...
Iterations of the loop are distributed between the threads in this example.
Compiling and Running a Parallel Version
Compile the program.
gcc array_multiply_omp.c -o array_multiply_omp -fopenmp
Run it on the cluster with 4 threads.
srun -c4 --mem=5000 array_multiply_omp
Using Threads
Run the program with different number of threads and observe how the runtime changes.
- What happens to the runtime when you change the number of threads?
For a loop to be parallelized, it must meet certain requirements
- An iteration count must be defined for the loop
- After the loop begins, the number of iterations cannot change.
- The loop cannot contain any calls to
break()orexit()functions.
Parallelizing while loops is not possible since the number of iterations is unknown.
Calculating the Sum of Matrix Elements
- Here is a basic example code:
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
int main(int argc, char **argv)
{
double start, end;
int size = 1e4;
int **A, *C;
int i, j;
/* Allocate memory */
C = malloc(size * sizeof(int));
A = (int **)malloc(size * sizeof(int *));
for (i = 0; i < size; i++)
A[i] = malloc(size * sizeof(int));
/* Set all matrix elements to 1 */
for (i = 0; i < size; i++)
for (j = 0; j < size; j++)
A[i][j] = 1;
/* Zero the accumulator */
for (i = 0; i < size; i++)
C[i] = 0;
start = omp_get_wtime();
#pragma omp parallel for
/* Each thread sums one column */
for (i = 0; i < size; i++)
for (j = 0; j < size; j++)
C[i] += A[i][j];
int total = 0;
/* Add sums of all columns together */
for (i = 0; i < size; i++)
total += C[i];
end = omp_get_wtime();
printf("Total is %d, time is %f s\n", total, end-start);
}
Are the matrix elements added up correctly?
- What result should this code produce?
- Is the code producing the expected result?
- What might be the problem? How can this be fixed?
Solution
- The elements all have value 1, and there are 1e4*1e4 of them, so the total should be 1e8.
- Sum of the matrix sum is incorrect.
- OpenMP threads share memory. This means that every thread has read and write access to all of the process memory. In this example, multiple threads are all accessing the loop variable j. Threads that started last will reset j and as a result threads that started earlier will count some elements more than once. For the code to work correctly each thread must have its own copy of the variable j.
The omp private clause
- Private variables are hidden from other threads.
#pragma omp parallel for private(j)
- In every thread, a private variable is created locally.
- When entering a parallel region, private copies of a variable are created from the original object.
There is an implicit way to make variables private or shared
- Variables declared outside of a parallel region are implicitly shared
- Variables declared inside are implicitly private.
Be Cautious About Data Dependencies
- If there is a data dependency between two statements, then the order in which those statements are executed may affect the output of the program, and hence its correctness.
Consider this loop that computes a cumulative sum:
for ( i = 2; i < N; i = i + 1 ) {
a[i] = a[i] + a[i-1];
}
The result will be incorrect if any two iterations are not performed in the right order
Types of Data Dependencies:
- FLOW (READ after WRITE), like the last example, when one statement uses the results of another.
- ANTI (WRITE after READ), when one statement should write to a location only ‘‘after’’ another has read what’s there.
- OUTPUT (WRITE after WRITE), when two statements write to a location, so the result will depend on which one wrote to it last.
- INPUT (READ after READ). Both statements read a variable. Since neither tasks writes, they can run in either order.
View wikipedia page on data dependencies
Identifying data dependencies
What loops have data dependencies?
/* loop #1 */ for ( i=2; i<N; i=i+2 ) { a[i] = a[i] + a[i-1]; } /* loop #2 */ for ( i=1; i<N/2; i=i+1 ) { a[i] = a[i] + a[i+N/2]; } /* loop #3 */ for ( i=0; i<N/2+1; i=i+1 ) { a[i] = a[i] + a[i+N/2]; } /* loop #4 */ for ( i=1; i<N; i=i+1 ) { a[idx[i]] = a[idx[i]] + b[idx[i]]; }Solution
Loop #1 does not. The increment of this loop is 2, so in the first step we compute a[2]=a[2]+a[1]. In the next step we compute a[4]=a[4]+a[3] … etc.
Loop #2 does not. In this example we are summing array elements separated by half array size. In this range of i values each thread modifies only one element of the array a.
Loop #3 does. Here the last iteration creates data dependency writing to a[N/2] because a[N/2] is used when i=0:i=N/2; a[N/2] = a[N/2] + a[N] i=0; a[0] = a[0] + a[N/2]Loop #4 might or might not, depending on the contents of the array idx. If any two entries of idx are the same, then there’s a dependency.
- Take a look at your code for data dependencies and eliminate them where you can.
- The method of writing into a new array and updating old from new after each iteration is one approach.
Thread-safe Functions
Consider this code:
#pragma omp parallel for
for(i = 0, i < N, i++)
y[i] = func(x[i])
Will this parallel code give the same results as the serial version?
- It depends on what the function does.
Thread-safe functions are those that can be called concurrently by multiple threads.
Consider the following function for calculating distance between two points in 2D:
float funct(float *p1, float *p2)
{
float dx, dy;
dx = p2[0]-p1[0];
dy = p2[1]-p1[1];
return(sqrt(dx*dx + dy*dy));
}
- This function is thread-safe because dx and dy are private.
Take a look at a modified version of the code in which dx and dy are defined externally:
float dx, dy;
float funct(float *p1, float *p2)
{
dx = p2[0]-p1[0];
dy = p2[1]-p1[1];
return(sqrt(dx*dx + dy*dy));
}
- This function is not thread-safe because dx and dy are global and can be modified by any thread.
It is important to be aware of whether the functions you use are thread-safe.
For more info, see Thread safety.
Optimizing Performance
CPU Cache and Data Locality
Let’s do a quick experiment. Compile our matrix_multiply_omp.c code with Intel compiler:
gcc matrix_multiply_omp.c -fopenmp -O1
Run on 4 CPUs and record timing. On our training cluster you will get something like:
srun --mem-per-cpu=2000 -c4 ./a.out
Total is 100000000, time is 0.014977 s
Then swap i and j indexes in the main for loop:
...
#pragma omp parallel for
for (i = 0; i<size; i++)
for (int j=0; j<size; j++)
C[i] += A[i][j]; /* <-- Swap indexes --- */
...
Recompile the program and run it again.
Total is 100000000, time is 0.391304 s
What is going on?
- CPU cache helps to accelerate computations by eliminating memory bottlenecks.
- To take advantage of CPU cache, an array we are looping through must be stored sequentially as a contiguous memory block.
If inner loop iterates through elements of a row then chunk of a row is loaded into cache upon the first access:
inner loop j (rows)
j=1 j=2
1 2 ... 1000 ... --> 1 2 ... 1000
1001 1002 ... 2000 ... --> 1001 1002 ... 2000
2001 2002 ... 3000 ...
...
This will not happen if in the inner loop we iterate through elements of a column (loop variable i) because columns are not contiguous memory blocks:
inner loop i (columns)
i=1 i=2
1 2 ... 1000 ... --> 1 1001 2001 ... 2 1002 2002 ...
1001 1002 ... 2000 ...
2001 2002 ... 3000 ...
...
In this case, CPU will need to access main memory to load each matrix element.
Avoiding Parallel Overhead at Low Iteration Counts
- Use conditional parallelization:
#pragma omp parallel for if(N > 1000)
for(i = 0; i < N; i++){
a[i] = k*b[i] + c[i];
}
Minimizing Parallelization Overhead
If the inner loop is parallelized, in each iteration step of the outer loop, a parallel region is created. This causes parallelization overhead.
- It’s better to create fewer threads with longer tasks.
Key Points
With the
parallel forpragma, a loop is executed in parallelWhen a variable is accessed by different threads, incorrect results can be produced.
Each thread receives a copy of the variable created by the
privateclause
Race Conditions with OpenMP
Overview
Teaching: 25 min
Exercises: 5 minQuestions
How can we calculate integrals in parallel?
How to compile a program using math functions with gcc?
Objectives
Understand what is a race condition
Learn how to avoid race conditions
Learn how to use reduction variables
- data race occurs when two threads access the same memory without proper synchronization.
- data race can cause a program to produce incorrect results in parallel mode.
Parallel Numerical Integration
Here is an example of an integration of the sine function from 0 to $\pi$.
Serial version is as follows:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char **argv) {
int steps = 1e7; /* Number of rectangles */
double delta = M_PI/steps; /* Width of each rectangle */
double total = 0.0; /* Accumulator */
int i;
printf("Using %.0e steps\n", (float)steps);
for (i=0; i<steps; i++) {
total = total + sin(delta*i) * delta;
}
printf("The integral of sine from 0 to Pi is %.12f\n", total);
}
Make a copy of the file integrate_sin_serial.c that you will work with to parallelize. You can call it integrate_sin_omp.c.
Compiling Code with Mathematical Functions
To compile a C program that uses math library with GCC we need to explicitly link to it:
gcc -o integrate integrate_sin_omp.c -lm
Let’s run the program.
./integrate
Using 1e+07 steps
The integral of sine from 0 to Pi is 2.000000000000
- Use the
timeutility to get the execution time:
srun time -p ./integrate
Using 1e+07 steps
The integral of sine from 0 to Pi is 2.000000000000
real 0.94
user 0.94
sys 0.00
The output real is the useful one. This example took 0.941 seconds to run.
The user and sys lines describe how much time was spent in the “user” code and how much in the “system” code, a distinction that doesn’t interest us today.
Parallelizing Numerical Integration
Let’s parallelize the main loop and execute the code.
...
printf("Using %.0e steps\n", (float)steps);
#pragma omp parallel for
...
integrate_sin_omp.c
- The result is incorrect because data dependency on total leads to a race condition when the program is run in parallel.
How to Avoid Data Race Conditions?
- Data races can be avoided by synchronizing threads so that variables are accessed in the correct order.
The omp critical Directive
Race conditions can be avoided by adding a critical directive.
- A critical directive only allows one thread at a time to run some block of code.
Add the omp critical directive to the statement in the main loop and rerun the code.
...
printf("Using %.0e steps\n", (float)steps);
#pragma omp parallel for
for (i=0; i<steps; i++) {
#pragma omp critical
...
integrate_sin_omp.c
gcc -o integrate integrate_sin_omp.c -lm -fopenmp
srun -c1 time -p ./integrate
srun -c2 time -p ./integrate
- Using critical, in this case, is a wrong decision because critical serializes the whole loop.
The omp atomic Directive
- The omp atomic directive is similar to critical but one thread being in an atomic operation doesn’t block any other atomic operations about to happen.
- The downsides:
- it can be used only to control a single statement
- the set of operations that atomic supports is restricted
- there are serialization costs associated with both omp critical and omp atomic.
Examples demonstrating how to use atomic:
#pragma omp atomic update
k += n*mass; /* update k atomically */
#pragma omp atomic read
tmp = c; /* read c atomically */
#pragma omp atomic write
count = n*m; /* write count atomically */
#pragma omp atomic capture
{ /* capture original value of v in d, then atomically update v */
d = v;
v += n;
}
The atomic clauses: update (default), write, read, capture
Parallel Performance
- Replace the critical directive with the atomic directive, recompile the code and run it on more that one thread. Try different number of threads (1-8) and record execution time.
- How execution time compares to the code using critical?
Solution
Version Threads Time serial 0.94 parallelized using critical 1 1.11 parallelized using critical 2 1.32 parallelized using critical 4 1.71 parallelized using atomic 1 1.03 parallelized using atomic 2 0.69 parallelized using atomic 4 0.72
The Optimal Way to Parallelize Integration
The best option is to let each thread work on its own chunk of data and then sum the sums of all threads. The reduction clause lets you specify thread-private variables that are subject to a reduction operation at the end of the parallel region
- the reduction operation for summation is is “+”
- at the end of the parallel construct the values of all private copies of the shared variable will be added together
#pragma omp parallel for reduction(+: total)
Recompile the code and execute. Now we got the right answer, and x3.7 speedup with 4 threads!
- Other reduction operators:
- subtraction
- multiplication
- minimum, maximum
- logical operators.
Finding the Maximum Value in an Array
Imagine that you are trying to find the largest value in an array. Is there a way to do this type of search in parallel? Begin with the serial version:
/* --- File array_max_serial.c --- */ #include <stdio.h> #include <stdlib.h> #include <omp.h> #include <math.h> int main(int argc, char **argv) { int size = 1e8; int *rand_nums; int i; int curr_max; time_t t; rand_nums=malloc(size*sizeof(int)); /* Intialize random number generator */ srand((unsigned) time(&t)); /* Initialize array with random values */ for (i=0; i<size; i++) { rand_nums[i] = rand(); } /* Find maximum */ curr_max = 0.0; for (i=0; i<size; i++) { curr_max = fmax(curr_max, rand_nums[i]); } printf("Max value is %d\n", curr_max); }Solution
This problem is analogous to the summation.
- Because the curr_max variable will be written to, each thread should have its own copy.
- Once all threads have found the maximum value in their share of data, you need to determine which thread has the largest value.
... curr_max = 0.0; #pragma omp parallel for reduction(max:curr_max) ...
Key Points
Race conditions can be avoided by using the omp critical or the omp atomic directives
The best option to parallelize summation is to use the reduction directive
OpenMP Tasks
Overview
Teaching: 25 min
Exercises: 5 minQuestions
How to recurse in parallel
Objectives
Use general parallel tasks
There are some fundamental limitations to the openmp constructs we have considered so far.
- only loops with a known length at run time are allowed
- finite number of parallel sections.
Some common computation tasks such as recursive or pointer-chasing algorithms and while loops are not compatible with these limitations.
The omp task
- The omp task directive was introduced in version 3.0 in 2008.
What is a task?
- A task is composed of the code to be executed and the data environment (inputs to be used and outputs to be generated).
Task execution model
- The execution of a task may be immediate or delayed.
- If delayed, the task in placed in a pool of tasks.
- All threads can take tasks out of the pool and execute them.
- Tasks need a scheduler.
- The implementation of the scheduling is compiler-specific.
- Need control of task generation.
A typical program using tasks would follow the code shown below:
/* Create threads */
#pragma omp parallel
{
#pragma omp single
{
for(i<1000) /* Generate tasks */
#pragma omp task
work_on(i)
}
}
- A parallel region creates a team of threads
- A single thread then creates the tasks, adding them to a pool that belongs to the team
- All the threads in that team execute tasks from this queue. Tasks could run in any order.
If you need to have results from the tasks before you can continue, you can use the taskwait directive to pause your program until the tasks are done.
Finding the Smallest Factor
Let’s use tasks to find the smallest factor of a large number (using 4993*5393 as test case). Start with the serial code:
#include <stdio.h>
#include <stdlib.h>
int main()
{
int N = 26927249;
int f;
for (f = 2; f <= N; f++)
{
if (f % 200 == 0) /* Print progress */
{
fprintf(stdout, "checking: %li\n", f);
fflush(stdout);
}
/* Check if f is a factor */
if (N % f == 0)
{ // The remainder is 0, found factor!
fprintf(stdout, "Factor: %li\n", f);
exit(0); /* Terminate the program */
}
for (int i = 1; i < 4e6; i++)
; /* Burn some CPU cycles */
/* End of factor finding block */
}
}
Exercise
Make the following changes to the code:
- Turn the factor finding block into a task.
- Generate a task for each trial factor.
- Once a factor is identified, stop generating tasks.
- Print the progress of tasks generation and execution separately.
Run the program in parallel and compare execution time with the serial version.
time srun ./factor time srun -c4 ./factor
- How many tasks are in the pool?
- How many tasks will be created if you submit a job with 100 and 400 threads?
- Are all tasks generated right away?
time srun -c4 --export OMP_NUM_THREADS=100 ./factorsolution
/* File find_factor_omp.c */ #include <stdio.h> #include <stdlib.h> int main() { long N = 4993 * 5393; long f; #pragma omp parallel #pragma omp single for (f = 2; f <= N; f++) /* Loop generating tasks */ { if (f % 200 == 0) /* Print progress */ { fprintf(stdout, "%li tasks generated\n", f); fflush(stdout); } #pragma omp task { /* Check if f is a factor */ if (f % 200 == 0) /* Print progress */ fprintf(stdout, " %li tasks done\n", f); if (N % f == 0) { // The remainder is 0, found factor! fprintf(stdout, "Factor: %li\n", f); exit(0); /* Terminate the program */ } else for (int i = 1; i < 4e6; i++) ; /* Burn some CPU cycles */ } } }Not all tasks are generated right away. To prevent overloading of the system, the scheduler controls the size of the task pool. As soon as the list of deferred tasks gets too long, the implementation stops generating new tasks, and switches all threads in the team to executing already generated tasks.
Task Synchronization
Some applications require tasks to be executed in a certain order.
For example, consider the code:
x = f();
#pragma omp task
{ y1 = g1(x); }
#pragma omp task
{ y2 = g2(x); }
z = h(y1) + h(y2);
- We need to wait until tasks computing y1 and y2 are finished before computing z.
- Use the omp taskwait directive:
x = f();
#pragma omp task
{ y1 = g1(x); }
#pragma omp task
{ y2 = g2(x); }
#pragma omp taskwait
z = h(y1) + h(y2);
This corrected code will generate two tasks and wait for both of them to be finished before computing z.
Controlling Task Execution Order
In some cases a task may depend on another task, but not on all generated tasks. The taskwait directive in this case is too restrictive.
#pragma omp task /* task A */
preprocess_data(A);
#pragma omp task /* task B */
preprocess_data(B);
#pragma omp taskwait
#pragma omp task /* task C */
compute_stats(A);
#pragma omp task /* task D */
compute_stats(B);
In the example above case task C should be executed after task A, but it won’t run until the execution of task B is finished.
The task depend clause enforces constraints on the scheduling of tasks. Only sibling tasks are dependent on each other under these constraints.
- The depend clause is followed by an access mode that can be in, out or inout.
- depend(in:x) - task will read variable x
- depend(out:y) - task will write variable y, previous value of y will be ignored.
- depend(inout:z) - task will both read and write variable z
- The OpenMP scheduler considers task dependencies and automatically decides whether a task is ready for execution.
The previous example rewritten with task dependencies will be:
#pragma omp task depend(out:A) /* task A */
preprocess_data(A);
#pragma omp task depend(out:B) /* task B */
preprocess_data(B);
#pragma omp task depend(in:A) /* task C */
compute_stats(A);
#pragma omp task depend(in:B) /* task D */
compute_stats(B);
This example illustrates READ after WRITE dependency: task A writes A, which is then read by task C.
Controlling Order of Data Access
Consider the following loop:
for(i=1;i<N;i++) for(j=1;j<N;j++) x[i][j] = x[i-1][j] + x[i][j-1];The loop cannot be parallelized with parallel for construct due to data dependency. The next task should be executed after the previous task updates the variable x.
- Use tasks with dependencies to parallelize this code.
- You should be able to correct the code by only adding the task depend clause.
- Start with the incorrectly parallelized code:
#include <stdlib.h> #include <stdio.h> int main(int argc, char **argv) { int N = 8; int x[N][N], y[N][N]; int i, j; /* Initialize x,y */ for (i = 0; i < N; i++) { x[0][i] = x[i][0] = y[0][i] = y[i][0] = i; } /* Serial computation */ for (i = 1; i < N; i++) { for (j = 1; j < N; j++) x[i][j] = x[i - 1][j] + x[i][j - 1]; } /* Parallel computation */ #pragma omp parallel #pragma omp single for (i = 1; i < N; i++) { for (j = 1; j < N; j++) #pragma omp task y[i][j] = y[i - 1][j] + y[i][j - 1]; } printf("Serial result:\n"); for (i = 0; i < N; i++) { for (j = 0; j < N; j++) printf("%6d", x[i][j]); printf("\n"); } printf("Parallel result:\n"); for (i = 0; i < N; i++) { for (j = 0; j < N; j++) printf("%6d", y[i][j]); printf("\n"); } }This example works correctly with gcc/9.3.0 but not with gcc/10 or gcc/11.
solution
Parallel threads are writing data, so the dependence should be depend(out:y)
Computing Fibonacci Numbers
The next example shows how task and taskwait directives can be used to compute Fibonacci numbers recursively. The Fibonacci Sequence is the series of numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … The next number is found by adding up the two numbers before it.
- In the parallel construct, the single directive calls fib(n).
- The call to fib(n) generates two tasks. One of the tasks computes fib(n-1) and the other computes fib(n-2).
- The two return values are added together to produce the value returned by fib(n).
- Each of the calls to fib(n-1) and fib(n-2) will in turn generate two tasks. Tasks will be recursively generated until the argument passed to fib() is less than 2.
The taskwait directive ensures that both tasks generated in fib( ) compute i and j before return.
#include <stdio.h> #include <stdlib.h> #include <omp.h> /* Usage: ./fib [n] */ /* Default n=10 */ int fib(int n) { int i, j; if (n<2) return n; else { #pragma omp task shared(i) i=fib(n-1); #pragma omp task shared(j) j=fib(n-2); #pragma omp taskwait return i+j; } } int main(int argc, char **argv){ int n=10, result; if(argc==2) { char *a = argv[1]; n = atoi(a); } #pragma omp parallel { #pragma omp single result = fib(n); } printf("Fibonacci number %d is %d\n", n, result); }
Tasks?
How do tasks work with different number of threads? Can OpenMP use more than one thread to execute a task?
Solution
Each task region will be executed by one thread. OpenMP will not use more threads to execute a single task.
Task gotchas
There are a few gotchas to be aware of. While the intention is that tasks will run in parallel, there is nothing in the specification that guarantees this behavior. You may need to check how your particular environment works.
Review
| OpenMP pragma, function, or clause | Concepts |
|---|---|
| #pragma omp parallel | Parallel region, teams of threads, structured block, interleaved execution across threads |
| int omp_get_thread_num() int omp_get_num_threads() |
Create threads with a parallel region and split up the work using the number of threads and thread ID |
| double omp_get_wtime() | Speedup and Amdahl’s law. Assessing performance |
| setenv OMP_NUM_THREADS N | Internal control variables. Setting the default number of threads with an environment variable |
| #pragma omp barrier #pragma omp critical |
Synchronization and race conditions. |
| #pragma omp for #pragma omp parallel for |
Worksharing, parallel loops, loop carried dependencies |
| reduction(op:list) | Reductions of values across a team of threads |
| schedule(dynamic [,chunk]) schedule (static [,chunk]) |
Loop schedules, loop overheads and load balance |
| private(list) firstprivate(list) shared(list) |
Data environment |
| nowait | Disabling implied barriers on workshare constructs, the high cost of barriers. |
| #pragma omp single | Workshare with a single thread |
| #pragma omp task #pragma omp taskwait |
Tasks including the data environment for tasks. |
Key Points
OpenMP can manage general parallel tasks
tasks now allow the parallelization of applications exhibiting irregular parallelism such as recursive algorithms, and pointer-based data structures.
Calculating Many-Body Potentials
Overview
Teaching: 20 min
Exercises: 5 minQuestions
How to speed up calculation leveraging both OpenMP and SIMD instructions
Objectives
Learn using automatic vectorization in Intel and GCC compilers
Learn about the schedule clause
The Algorithm
To compute total electrostatic potential energy we need to sum interactions between all pairs of charges:
[E = \sum\frac{charge_i*charge_j}{distance_{i,j}}]
Let’s consider a simple nano crystal particle with a cubic structure.
- The model has n atoms per side
- The lattice constant a = 0.5 nm
- The charges of atoms are randomly assigned with values between -5 and 5 a.u.
Let’s start with the following serial code:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
int main(int argc, char **argv)
{
struct timespec ts_start, ts_end;
float time_total;
int n = 60; /* number of atoms per side */
int n_charges = n * n * n; /* total number of charges */
float a = 0.5; /* lattice constant a (a=b=c) */
float *q; /* array of charges */
float *x, *y, *z; /* x,y,z coordinates */
float dx, dy, dz, dist; /* temporary pairwise distances */
double Energy = 0.0; /* potential energy */
int i, j, k;
q = malloc(n_charges * sizeof(float));
x = malloc(n_charges * sizeof(float));
y = malloc(n_charges * sizeof(float));
z = malloc(n_charges * sizeof(float));
/* Seed random number generator */
srand(111);
/* initialize coordinates and charges */
int l = 0;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
for (k = 0; k < n; k++)
{
x[l] = i * a;
y[l] = j * a;
z[l] = k * a;
/* Generate random numbers between -5 and 5 */
q[l] = 10 * ((double)random() / (double)RAND_MAX - 0.5);
l++;
}
/* Calculate sum of all pairwise interactions: q[i]*q[j]/dist[i,j] */
clock_gettime(CLOCK_MONOTONIC, &ts_start);
for (i = 0; i < n_charges; i++)
{
for (j = i + 1; j < n_charges; j++)
{
dx = x[i] - x[j];
dy = y[i] - y[j];
dz = z[i] - z[j];
dist = sqrt(dx * dx + dy * dy + dz * dz);
Energy += q[i] * q[j] / dist;
}
}
clock_gettime(CLOCK_MONOTONIC, &ts_end);
time_total = (ts_end.tv_sec - ts_start.tv_sec) * 1e9 + (ts_end.tv_nsec - ts_start.tv_nsec);
printf("\nTotal time is %f ms, Energy is %.3f\n", time_total / 1e6, Energy * 1e-4);
}
Our goal is to speed up calculation leveraging OpenMP and SIMD instructions (vectorization).
Performance Considerations
Serial Performance
First we need to compile the serial version to use as a reference for calculation of parallel scaling. For this section we will use Intel compiler.
Using the Auto-vectorizer in Intel Compilers
At optimization levels -O2 or higher Intel compiler automatically tries to vectorize code. To compile an unvectorized version with the same optimization level we need to turn off auto vectorization.
- disable auto-vectorizer (-no-vec)
How do we know if compiler was able to vectorize any loops?
For this we will use a couple of new compiler options:
- turn on optimization reporting (-qopt-report=1)
- turn on vectorization report (-qopt-report-phase=vec).
module load intel/2022.1.0
icc -qopt-report=1 -qopt-report-phase=vec -O3 -no-vec elect_energy_serial.c
srun -c1 ./a.out
Intel compiler does not print optimization information on screen, it creates optimization report *.optrpt files.
Optimization report saved in the file elect_energy.optrpt indicates that our main nested for loops computing potential energy at lines 42 and 44 are not vectorized:
LOOP BEGIN at elect_energy.c(42,2)
remark #25460: No loop optimizations reported
LOOP BEGIN at elect_energy.c(44,3)
remark #25460: No loop optimizations reported
LOOP END
LOOP END
This is what we wanted for the reference serial code. Let’s run it and record execution time.
srun -c1 ./a.out
The runtime of the serial version is about 80 sec on a real cluster with Skylake CPUs. It will run somewhat slower on the training cluster.
Using the auto-vectorizer in GCC
- auto-vectorizer is enabled by default at optimization level -O3
- auto-vectorizer can be enabled with the option -ftree-vectorize and disabled with -fno-tree-vectorize
- print info about unsuccessful optimization -fopt-info-vec-missed
- print info about optimized loops -fopt-info-vec-optimized
Parallel Performance
Using Automatic Vectorization
Next we will use use the auto-vectorizer in the compiler. This means do nothing except ensuring that the coding will not prevent vectorization. Many things, can prevent automatic vectorization or produce suboptimal vectorized code.
- Recompile the code without -no-vec option.
The optimization report indicates that the inner for loop at line 44 is now vectorized:
LOOP BEGIN at elect_energy.c(44,3)
remark #15300: LOOP WAS VECTORIZED
LOOP END
The auto vectorized program runs in about 26 sec on the real cluster. This is some improvement, but not very impressive. The speedup relative to the serial version is only about 3x. Skylake CPUs are able to process 16 floating pointing numbers simultaneously, so theoretical speedup should be 16x, right? Can we do better?
- By default, the compiler uses avx2 instructions.
- Enforce using avx512 instructions: -march=skylake.
On the training cluster this version will run only on “c” or “g” flavour nodes because only these flavours have Skylake CPUs supporting AVX-512.
- AVX-512 nodes can be requested using the –nodelist option, e.g.
srun --nodelist=large-node1 ./a.out
Now the program runs in 15.7 sec (on the real cluster), this is better (5x speedup), but still does not live up to our expectations. Can we do better?
- Yes, if we parallelize explicitly using Intrinsic AVX Functions.
Using Intel’s Advanced Vector Extensions (AVX) Intrinsic Functions.
This is not too complicated, and worth doing because you will be able to decide how you data is organized, moved in and out of vector processing units and what AVX instructions are used for calculations. With Intrinsic Functions, you are fully responsible for design and optimization of the algorithm, compiler will follow your commands.
The examples of the same program written with AVX2 and AVX-512 Intrinsics are in the files elect_energy_avx2.c and elect_energy_avx512.c, respectively. The code is well annotated with explanations of all statements.
To summarize the vectorized algorithm:
- allocate memory for _m512 vectors, each one hold 16 floating point values
- memory must be aligned with 64 byte margins for optimal transfer
- pack data into _m512 vectors
- accumulate interactions looping over 16x16 tiles
Compile the code and run it.
icc -qopt-report=1 -qopt-report-phase=vec -O3 elect_energy_avx2.c
srun ./a.out
On the real cluster the code with explicit AVX2 instructions is twice faster than the auto-vectorized AVX-512 version,so this is 10x faster than the serial code.
But we can do even better. Try the AVX-512 version. AVX-512 registers are twice wider than AVX2; they can operate on 16 floating point numbers.
Compile the code and run it.
icc -qopt-report=1 -qopt-report-phase=vec -O3 elect_energy_avx512.c
srun ./a.out
The benchmark on all versions on the real cluster is below. As you can see, AVX-512 version is 1.7x faster than AVX2. Adapting AVX2 to AVX-512 is very straightforward.
Benchmark n=60, Single Thread, Cluster Siku
| Version | Time | Speedup |
|---|---|---|
| Serial | 81.2 | 1.0 |
| auto-vec | 26.1 | 3.1 |
| auto-vec, skylake | 15.7 | 5.2 |
| avx2 | 7.7 | 10.5 |
| avx512 | 4.58 | 17.7 |
Compilers are very conservative in automatic vectorization and in general they will use the safest solution. If compiler suspects data dependency, it will not parallelize code. The last thing compiler developers want is for a program to give the wrong results! But you can analyze the code, if needed modify it to eliminate data dependencies and try different parallelization strategies to optimize the performance.
What Loops can be Vectorized?
- The number of iterations must be known (at runtime, not at compilation time) and remain constant for the duration of the loop.
- The loop must have single entry and single exit. For example no data-dependent exit.
- The loop must have straight-line code.
Because SIMD instructions perform the same operation on data elements it is not possible to switch instructions for different iterations. The exception is if statements that can be implemented as masks. For example the calculation is performed for all data elements, but the result is stored only for those elements for which the mask evaluates to true.
- No function calls are allowed. Only intrinsic vectorized math functions or functions that can be inlined are allowed.
Adding OpenMP Parallelization
The vectorized program can run in parallel on each of the cores of modern multicore CPUs, so the maximum theoretical speedup should be proportional to the numbers of threads.
Parallelize the Code
- Decide what variable or variables should be made private, and then compile and test the code.
- Run on few different numbers of CPUs. How does the performance scale?
Solution
Add the following OpenMP pragma just before the main loop
#pragma omp parallel for private(j, dx, dy, dz, dist) reduction(+:Energy) schedule(dynamic)
The benchmark on all versions on the real cluster is below. The speedup of the OpenMP version matches our expectations.
Benchmark n=60, OpenMP 10 Threads, Cluster Siku.
| Version | Time | Speedup |
|---|---|---|
| not vectorized | 7.8 | 10.4 |
| auto-vect | 2.5 | 32.5 |
| auto-vect, skylake | 1.43 | 56.8 |
| avx2 | 0.764 | 106.3 |
| avx512 | 0.458 | 177.3 |
OpenMP Scheduling
- In static scheduling all iterations are allocated to threads before they execute any loop iterations.
- In dynamic scheduling, OpenMP assigns one iteration to each thread. Threads that complete their iteration will be assigned the next iteration that hasn’t been executed yet.
OpenMP automatically partitions the iterations of a parallel for loop. By default it divides all iterations in a number of chunks equal to the number of threads. The number of iterations in each chunk is the same, and each thread is getting one chunk to execute. This is static scheduling, in which all iterations are allocated to threads before they execute any loop iterations. However, a static schedule can be non-optimal. This is the case when the different iterations need different amounts of time. This is true for our program computing potential. As we are computing triangular part of the interaction matrix static scheduling with the default chunk size will lead to uneven load.
This program can be improved with a dynamic schedule. In dynamic scheduling, OpenMP assigns one iteration to each thread. Threads that complete their iteration will be assigned the next iteration that hasn’t been executed yet. The allocation process continues until all the iterations have been distributed to threads.
- If dynamic scheduling balances load why would we want to use static scheduling at all?
The problem is that here is some overhead to dynamic scheduling. After each iteration, the threads must stop and receive a new value of the loop variable to use for its next iteration. Thus, there’s a tradeoff between overhead and load balancing.
- Static scheduling has low overhead but may be badly balanced
- Dynamic scheduling has higher overhead.
Both scheduling types also take a chunk size argument; larger chunks mean less overhead and greater memory locality, smaller chunks may mean finer load balancing. Chunk size defaults to 1 for dynamic schedule and to $\frac{N_{iterrations}}{N_{threads}}$ for static schedule.
Let’s add a schedule(dynamic) or schedule(static,100) clause and see what happens.
Experiment with Scheduling
- Try different scheduling types. How does it affect the performance? What seems to work best for this problem? Can you suggest the reason?
- Does the optimal scheduling change much if you grow the problem size? That is, if you make n bigger?
- There’s a third scheduling type, guided, which starts with large chunks and gradually decreases the chunk size as it works through the iterations. Try it out too, if you like. With the guided scheduling, the chunk parameter is the smallest chunk size OpenMP will try.
Solution
We are computing triangular part of the interaction matrix. The range of pairwise interactions computed by a thread will vary from 1 to (n_charges - 1). Therefore, static scheduling with the default chunk size will lead to uneven load.
Example of the Code that can be Vectorized:
/* File: vectorize_1.c */ #include <stdlib.h> #include <stdio.h> #include <time.h> int main() { struct timespec ts_start, ts_end; float time_total; int i,j; long N=1e8; /* Size of test array */ float a[N], b[N], c[N]; /* Declare static arrays */ /* Generate some random data */ for(i=0;i<N;i++) { a[i]=random(); b[i]=random(); } printf("Test arrays generated\n"); /* Run test 3 times, compute average execution time */ float average_time=0.0f; for(int k=0;k<3;k++) { clock_gettime(CLOCK_MONOTONIC, &ts_start); for(int j=0;j<50;j++) for(i=0;i<N;i++) c[i]=a[i]*b[i]+j; clock_gettime(CLOCK_MONOTONIC, &ts_end); time_total = (ts_end.tv_sec - ts_start.tv_sec)*1e9 + \ (ts_end.tv_nsec - ts_start.tv_nsec); printf("Total time is %f ms\n", time_total/1e6); average_time+=time_total; } printf("Average time is %f ms\n", average_time/3e6); }
Key Points
Writing vectorization-friendly code can take additional time but is mostly worth the effort
Different loop scheduling may compensate for unbalanced loop iterations
Programming GPUs with OpenMP
Overview
Teaching: 35 min
Exercises: 5 minQuestions
How to program GPU with OpenMP?
Objectives
Learn about tools available for programming GPU
Learn about programming GPU with openMP
Introduction to OpenMP Device Offload
- GPUs can deliver very high performance per compute node.
- Computing workloads are often accelerated by GPUs in HPC clusters.
The GPU Architecture
-
CPUs are designed to handle a wide-range of tasks quickly, but are limited in the number of tasks that can be running concurrently.
-
GPUs consist of thousands of smaller and more specialized processing units (cores).
Nvidia calls its parallel processing platform Compute Unified Device Architecture (CUDA).
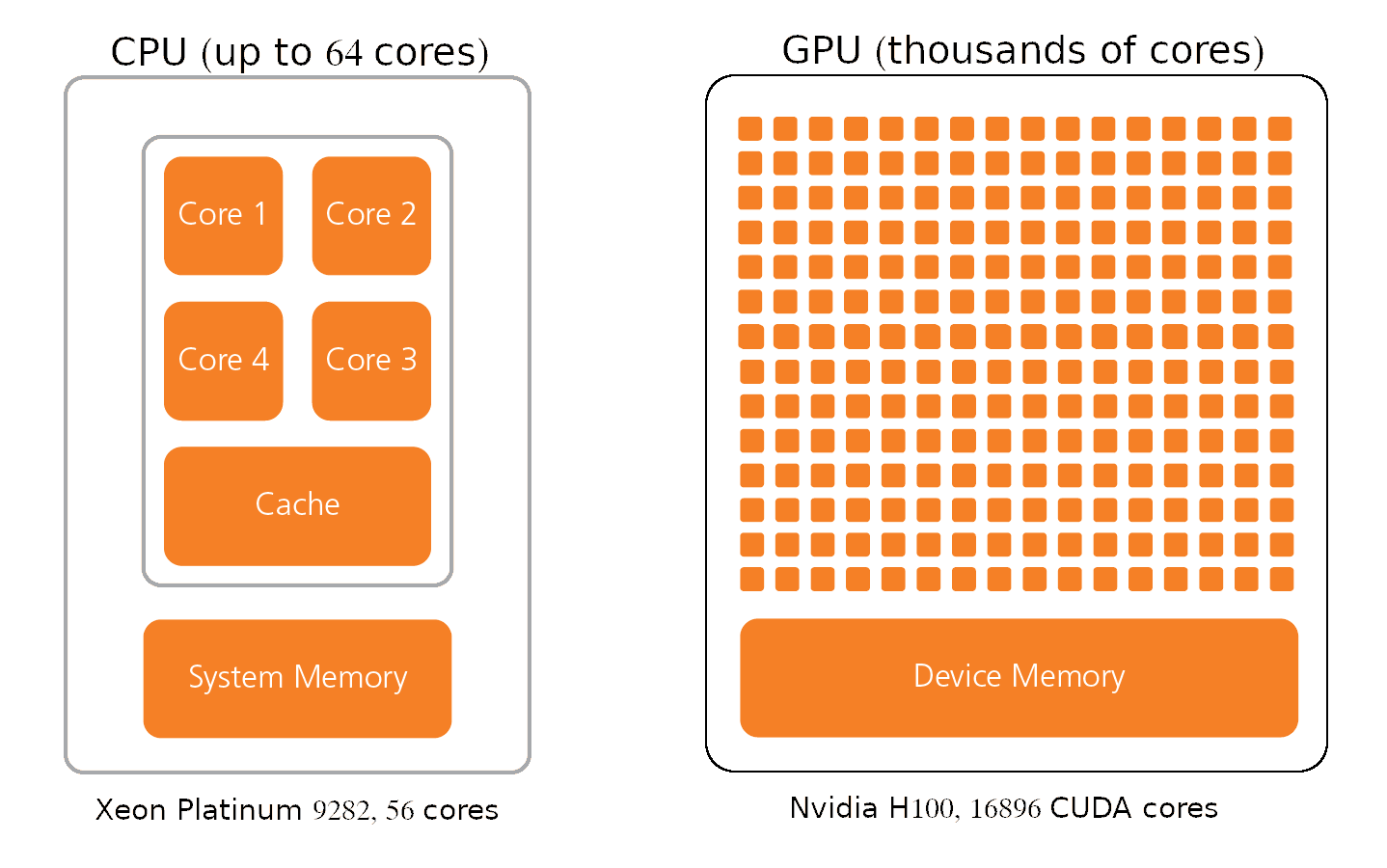
- Nvidia H100 GPUs
- up to 132 Streaming Multiprocessors
- 128 FP32 CUDA cores per SM
- total 16896 CUDA cores.
- Intel® Xeon® Platinum 9282
- 56 cores
- 1 AVX-512 vector unit per core can process 16 FP32 numbers at a time.
GPU architecture enables to process massive amounts of data simultaneously at extremely fast speeds.
Tools for Programming GPUs
There are several tools available for programming GPU.
- CUDA is NVIDIA-specific programming model and language. With CUDA, you can maximize your program performance. CUDA requires significant refactoring of existing C/C++ or Fortran code.
- PyCuDA. Gives access to CUDA functionality from Python code.
- OpenCL. Programs written in OpenCL can run on CPUs, GPUs, FPGAs, and other hardware accelerators. Very complex and hard to program, not widely used.
- OpenMP and OpenACC. Directive-based, offer a quick path to accelerated computing with less programming effort.
Read more about OpenMP on GPUs
Differences between OpenMP and OpenACC
- OpenMP approach is more prescriptive, programmers tell compiler explicitly where and how to parallelize the code
- OpenACC programs are more descriptive of parallelism and rely more on the compiler to implement the parallelism efficiently.
The OpenMP GPU programming model
GPU programming with OpenMP is based on a host-device model.
- The host is where the initial thread of a program begins to run.
- The host can be connected to one or more GPU devices.
- Each Device is composed of one or more Compute Units
- Each Compute Unit is composed of one or more Processing Elements
- Memory is divided into host memory and device memory
How many devices are available?
The omp_get_num_devices routine returns the number of target devices.
#include <stdio.h>
#include <omp.h>
int main()
{
int num_devices = omp_get_num_devices();
printf("Number of devices: %d\n", num_devices);
}
Compile with gcc/9.3.0:
module load gcc/9.3.0
gcc device_count.c -fopenmp -odevice_count
Run it on the login node. How many devices are available on the login node?
Then run it on a GPU node:
srun --gpus-per-node=1 ./device_count
Request two GPUs. How many devices are detected now?
How to offload to a GPU?
- Identify routines (compute kernels) suitable for accelerators.
- Explicitly express parallelism in the kernel.
- Manage data transfer between CPU and Device.
Example: compute sum of two vectors.
Start from the serial code vadd_gpu_template.c.
/* Compute sum of vectors A and B */
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
int main(int argc, char *argv[])
{
double start, end;
int size = 1e8;
float *A;
float *B;
float *C;
double sum = 0.0f;
int ncycles=atoi(argv[1]);
A = (float *)malloc(size * sizeof(float *));
B = (float *)malloc(size * sizeof(float *));
C = (float *)malloc(size * sizeof(float *));
/* Initialize vectors */
for (int i = 0; i < size; i++)
{
A[i] = (float)rand() / RAND_MAX;
B[i] = (float)rand() / RAND_MAX;
}
start = omp_get_wtime();
for (int k = 0; k < ncycles; k++)
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
end = omp_get_wtime();
printf("Time: %f seconds\n", end - start);
sum = sum / size;
printf("Sum = %f\n ", sum / ncycles);
}
gcc vadd_gpu_template.c -fopenmp -O3 -ovadd_serial
In order to get an accurate timing on GPUs, we must run summation multiple times. The number of repeats can be specified on the command line:
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_serial 10
Execution time of the serial code is around 1.6 sec.
How to Offload: the OpenMP Target Directive
- OpenMP offload constructs were introduced in OpenMP 4.0.
OpenMP target instructs the compiler to generate a target task, which executes the enclosed code on the target device.
Make a copy of the code:
cp vadd_gpu_template.c vadd_gpu.c
Identify code block we want to offload to GPU and generate a target task:
...
for (int k = 0; k < ncycles; k++)
#pragma omp target
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 10
libgomp: cuCtxSynchronize error: an illegal memory access was encountered
The compiler created target task and offloaded it to a GPU, but the data is on the host!
Moving Data Between Hosts and Devices: the OpenMP Map Directive.
map(map-type: list[0:N])
- map-type may be to, from, tofrom, or alloc. The clause defines how the variables in list are moved between the host and the device.
...
for (int k = 0; k < ncycles; k++)
#pragma omp target map(to: A[0:size],B[0:size]) map(from: C[0:size])
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 1
Execution time of the offloaded code is slower, around 8 sec. It is expected because:
- By using the
omp targetdirective, a target task is created, offloaded to the GPU, but is not parallelized. It executes on a single thread. - The processors on GPUs are slower than the CPUs.
- It takes some time for data to be transferred from the host to the device.
The OpenMP Teams directive.
teamsconstruct creates a league of teams.- the master thread of each team executes the code
Using the teams construct is the first step to utilizing multiple threads on a device. A teams construct creates a league of teams. Each team consists of some number of threads, when the directive teams is encountered the master thread of each team executes the code in the teams region.
...
for (int k = 0; k < ncycles; k++)
#pragma omp target teams map(to: A[0:size],B[0:size]) map(from: C[0:size])
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 1
Execution time is the same!
Now we have multiple threads executing on the device, however they are all performing the same work.
It is also important to note that only the master thread for each team is active.
Review
Right now we have:
- Multiple thread teams working on a device
- All thread teams are performing the same work
- Only the master thread of each team is executing
The OpenMP Distribute directive.
The distribute construct can be used to spread iterations of a loop among teams.
...
for (int k = 0; k < ncycles; k++)
#pragma omp target teams distribute \
map(to: A[0:size],B[0:size]) map(from: C[0:size])
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 1
Execution time is faster, about 1 sec, but how it compares with the CPU version?
gcc vadd_gpu_template.c -O3 -fopenmp -ovadd_serial
srun --mem=5000 -c4 ./vadd_serial 1
This is disappointing, serial version running on a single CPU is 5 times faster!
The master thread is the only one we have used so far out of all the threads available in a team!
At this point, we have teams performing independent iterations of this loop, however each team is only executing serially. In order to work in parallel within a team we can use threads as we normally would with the basic OpenMP usage. Composite constructs can help.
The distribute parallel for construct specifies a loop that can be executed in parallel by multiple threads that are members of multiple teams.
...
for (int k = 0; k < ncycles; k++)
#pragma omp target teams distribute \
parallel for \
map(to: A[0:size],B[0:size]) map(from: C[0:size])
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 1
Now, we have teams splitting the work into large chunks on the device, while threads within the team will further split the work into smaller chunks and execute in parallel.
We have two problems:
- It did not take less time to execute.
- The sum is not calculated correctly.
Maybe the work is not large enough for the GPU? To increase the amount of calculations, we could repeat the loop multiple times. Try running 20 cycles of addition. Did the execution time increase 20 times? It took only 7 seconds instead of the expected 20 seconds. We are on the right track, but what else can be improved in our code to make it more efficient?
The OpenMP Target Data directive.
Each time we iterate, we transfer data from the host to the device, and we pay a high cost for data transfer. Arrays A and B can only be transferred once at the beginning of calculations, and the results can only be returned to the host once the calculations are complete. The target data directive can help with this.
The target data directive maps variables to a device data environment for the extent of the region.
...
#pragma omp target data map(to: A[0:size], B[0:size]) map(from: C[0:size])
for (int k = 0; k < ncycles; k++)
#pragma omp target teams distribute \
parallel for \
map(tofrom: sum)
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
Compile and run on a GPU node for 20 cycles:
gcc vadd_gpu.c -fopenmp -O3 -ovadd_gpu
srun --gpus-per-node 1 --mem=5000 -c4 ./vadd_gpu 20
The time decreased from 7 to 1 sec! Try running for 100 cycles. Did the time increase proportionally to the work?
Let’s take care of issue with sum.
We get the wrong result with sum, it is zero, so it looks like it is not transferred back from the device.
...
#pragma omp target data map(to: A[0:size], B[0:size]) map(from: C[0:size])
for (int k = 0; k < ncycles; k++)
#pragma omp target teams distribute \
parallel for \
map(tofrom: sum) reduction(+:sum)
for (int i = 0; i < size; i++)
{
C[i] = A[i] + B[i];
sum += C[i];
}
...
We need to add a reduction clause and map sum tofrom the device since we parallelized the for loop.
Using Nvidia HPC compiler
Nvidia HPC compiler generates faster binary, but it does not run on the training cluster.
module load nvhpc/22.7
nvc vadd_gpu.c -O3 -fopenmp -mp=gpu -Minfo=mp
nvc vadd_gpu.c -O3 -fopenmp -mp=multicore -Minfo=mp
Getting info about available GPUs
Using the nvidia-smi command
nvidia-smi --query-gpu=timestamp,utilization.gpu,utilization.memory -format=csv -l 1 >& gpu.log&
Using OpenMP functions
#include <stdio.h>
#include <omp.h>
int main()
{
int nteams, nthreads;
int num_devices = omp_get_num_devices();
printf("Number of available devices %d\n", num_devices);
#pragma omp target teams defaultmap(tofrom : scalar)
{
if (omp_is_initial_device())
printf("Running on host\n");
else
{
nteams = omp_get_num_teams();
#pragma omp parallel
#pragma omp single
if (!omp_get_team_num())
{
nthreads = omp_get_num_threads();
printf("Running on device with %d teams x %d threads\n", nteams, nthreads);
}
}
}
}
Compile with gcc/9.3.0:
module load gcc/9.3.0
gcc get_device_info.c -fopenmp -ogpuinfo
srun --gpus-per-node=1 --mem=1000 ./gpuinfo
With gcc/11 you will get 216 teams x 8 threads (Quadro RTX 6000)
Compile with nvidia compiler:
module load nvhpc/22.7
nvc get_device_info.c -mp=gpu -ogpuinfo
srun --gpus-per-node=1 --mem=1000 ./gpuinfo
With nvhpc you’ll get 72 teams x 992 threads on the same GPU.
Parallelizing with OpenACC
cp vadd_gpu_template.c vadd_gpu_acc.c
The acc kernels Construct
Let’s add a single, simple OpenACC directive before the block containing for loop nest.
#pragma acc kernels
This pragma tells the compiler to generate parallel accelerator kernels (CUDA kernels in our case).
Compiling with Nvidia HPC SDK
Load the Nvidia HPC module:
module load StdEnv/2020 nvhpc/22
To compile the code with OpenACC we need to add the -acc flag
nvc vadd_gpu_acc.c -O3 -acc
Let’s run the program. It runs slow compared even to our serial CPU code.
Were the loops parallelized?
- enable printing information about the parallelization ( add the option -Minfo=accel) and recompile
nvc vadd_gpu_acc.c -O3 -acc -Minfo=accel
33, Generating implicit copyin(A[:100000000],B[:100000000]) [if not already present]
Generating implicit copy(sum) [if not already present]
Generating implicit copyout(C[:100000000]) [if not already present]
35, Complex loop carried dependence of B->,A-> prevents parallelization
Loop carried dependence due to exposed use of C prevents parallelization
Complex loop carried dependence of C-> prevents parallelization
Accelerator serial kernel generated
Generating NVIDIA GPU code
35, #pragma acc loop seq
36, #pragma acc loop seq
35, Complex loop carried dependence of C-> prevents parallelization
36, Complex loop carried dependence of B->,A->,C-> prevents parallelization
The __restrict Type Qualifier
Our data arrays (A, B, C) are dynamically allocated and are accessed via pointers. Pointers may create data dependency because:
- More than one pointer can access the same chunk of memory in the C language.
- Arithmetic operations on pointers are allowed.
Using the __restrict qualifier to a pointer ensures that it is safe and enables better optimization by the compiler.
float * __restrict A;
float * __restrict B;
float * __restrict C;
After this modification The compiler parallelizes the loop and even automatically determines what data should be copied to the device and what reduction operations are needed.
- It is important to examine optimixzation reports
- It is best to add explicit data transfer direcives and reduction clauses to ensure your program will work correctly when compiled with different compilers.
Key Points
OpenMP offers a quick path to accelerated computing with less programming effort
Introduction to GPU Programming with OpenACC
Overview
Teaching: 35 min
Exercises: 5 minQuestions
How to program GPU with OpenACC?
Objectives
Learn about programming GPU with openACC
Examples of OpenACC accelerated applications:
- VASP 6 (ab initio atomic scale modeling).NVIDIA GPU Accelerated VASP 6 uses OpenACC to Deliver 15X More Performance
- TINKER 9 (molecular dynamics)
OpenACC Compilers
- GCC
- PGI
- Nvidia HPC SDK
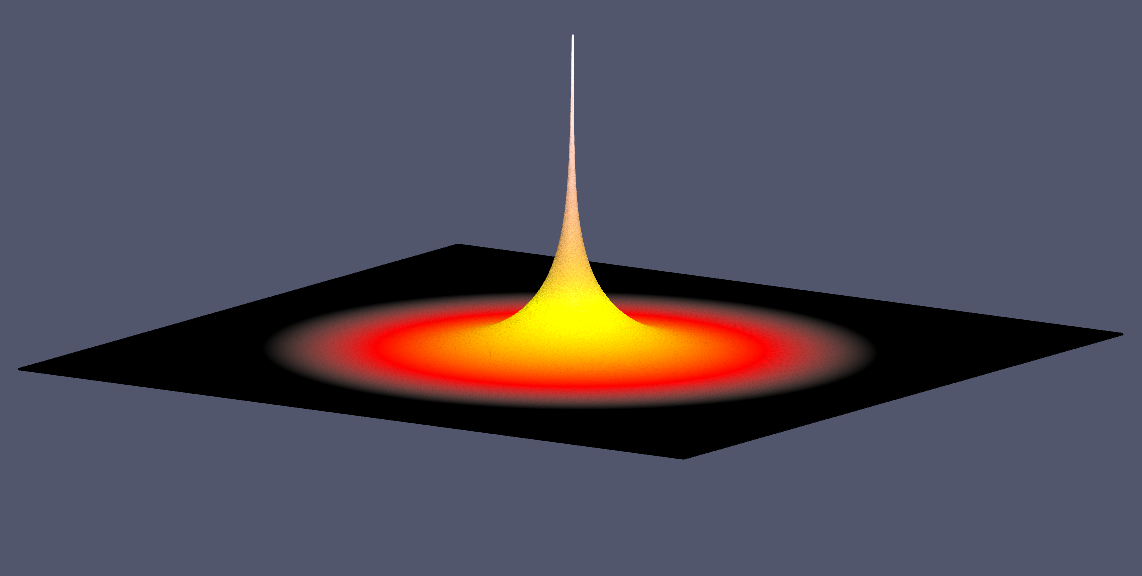
Solving the Discrete Poisson’s Equation Using Jacobi’s Method.
Poisson’s equation arises in heat flow, diffusion, electrostatic and gravitational potential, fluid dynamics, .. etc. The governing equations of these processes are partial differential equations, which describe how each of the variables changes as a function of all the others.
[\nabla^2U(x,y)=f(x,y)]
Here $ \nabla $ is the discrete Laplace operator, $ f(x,y) $ is a known function, and $ U(x,y) $ is the function to be determined.
This equation describes, for example, steady-state temperature of a uniform square plate. To make a solution defined we need to specify boundary conditions, i.e the value of $ U $ on the boundary of our square plate.
- We will consider the simple case with the boundaries kept at temperature $ U = 0 $.
- We will place a continuous point heat source in the middle of the plate ($ f(x,y)=0 $ everywhere except one hot spot in the middle of the plate.).
Jacobi’s Stencil in 2D.
- Common useful iterative algorithm.
- For discretization on a uniform spatial grid $ n\times m $ the solution can be found by iteratively computing next value at the grid point $ i,j $ as an average of its four neighboring values and the function $ f(i,j) $.
[U(i,j,m+1) = ( U(i-1,j,m) + U(i+1,j,m) + U(i,j-1,m) + U(i,j+1,m) + f(i,j) )/4]
Solution
Serial Jacobi Relaxation Code
/* File: laplace2d.c */
#include <math.h>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char **argv)
{
FILE *output_unit;
int i, j;
int n = 1024;
int m = 1024; /* Size of the mesh */
int qn = (int)n * 0.5; /* x-coordinate of the point heat source */
int qm = (int)m * 0.5; /* y-coordinate of the point heat source */
float h = 0.05; /* Instantaneous heat */
int iter_max = 1e8; /* Maximum number of iterations */
const float tol = 1e-6f; /* Tolerance */
struct timespec ts_start, ts_end;
float time_total;
float ** U, **U_new;
float ** F;
/* Allocate memory */
F = (float **)malloc(m * sizeof(float *)); /* Heat source array */
for (i = 0; i < m; i++)
F[i] = malloc(n * sizeof(float));
F[qn][qm] = h; /* Set point heat source */
U = (float **)malloc(m * sizeof(float *)); /* Plate temperature */
for (i = 0; i < m; i++)
U[i] = malloc(n * sizeof(float));
U_new = (float **)malloc(m * sizeof(float *)); /* Temporary new temperature */
for (i = 0; i < m; i++)
U_new[i] = malloc(n * sizeof(float));
printf("Jacobi relaxation calculation: %d x %d mesh\n", n, m);
/* Get calculation start time */
clock_gettime(CLOCK_MONOTONIC, &ts_start);
/* The main loop */
int iter = 0; /* Iterration counter */
float error = 1.0f; /* The initial error */
while (error > tol && iter < iter_max)
{
error = 0.f;
/* Compute the new temperature at the point i,j as a weighted average of */
/* the four neighbors and the heat source function F(i,j) */
{
for (j = 1; j < n - 1; j++)
{
for (i = 1; i < m - 1; i++)
{
U_new[j][i] = 0.25f * (U[j][i + 1] + U[j][i - 1] + U[j - 1][i] + U[j + 1][i]) + F[j][i];
error = fmaxf(error, fabsf(U_new[j][i] - U[j][i]));
}
}
/* Update temperature */
for (int j = 1; j < n - 1; j++)
{
for (i = 1; i < m - 1; i++)
U[j][i] = U_new[j][i];
}
if (iter % 200 == 0) /* Print error every 200 iterrations */
printf("%5d, %0.6e\n", iter, error);
iter++;
}
}
/* Get end time */
clock_gettime(CLOCK_MONOTONIC, &ts_end);
time_total = (ts_end.tv_sec - ts_start.tv_sec) * 1e9 + (ts_end.tv_nsec - ts_start.tv_nsec);
printf("\nTotal relaxation time is %f sec\n", time_total / 1e9);
/* Write data to a binary file for paraview visualization */
char *output_filename = "poisson_1024x1024_float32.raw";
output_unit = fopen(output_filename, "wb");
for (j = 0; j < n; j++)
fwrite(U[j], m * sizeof(float), 1, output_unit);
fclose(output_unit);
}
Performance of the Serial Code
Compile and run
gcc laplace2d_template.c -lm -O3
The serial code with 2048x2048 mesh does 10,000 iterations in 233 sec. Are the for loops at lines 50, 52, 59, and 61 vectorized?
gcc laplace2d.c -lm -O3 -fopt-info-vec-missed
Performance of the Auto-vectorized Code
Try Intel compiler:
module load intel/2022.1.0
icc -qopt-report=1 -qopt-report-phase=vec -O3 laplace2d.c
Only the for loop at line 52 is vectorized, the code runs in 136 sec.
Parallelizing Jacobi Relaxation Code with OpenACC
The acc kernels Construct
Let’s add a single, simple OpenACC directive before the block containing for loop nests at lines 50 and 59.
#pragma acc kernels
This pragma tells the compiler to generate parallel accelerator kernels (CUDA kernels in our case) for the block of loop nests following the directive.
Compiling with Nvidia HPC SDK
Load the Nvidia HPC module:
module load StdEnv/2020 nvhpc/20.7 cuda/11.0
To compile the code with OpenACC we need to add a couple of options:
- tell the nvc compiler to compile OpenACC directives (-acc)
- compile for target architecture NvidiaG Tesla GPU (-ta=tesla)
nvc laplace2d.c -O3 -acc -ta=tesla
Let’s run the program. Uh oh, that’s a bit of a slow-down compared even to our serial CPU code.
Were the loops parallelized?
- enable printing information about the parallelization ( add the option -Minfo=accel) and recompile
nvc laplace2d.c -O3 -acc -ta=tesla -Minfo=accel
50, Complex loop carried dependence of U->->,F->->,U_new->-> prevents parallelization
52, Complex loop carried dependence of U->->,F->->,U_new->-> prevents parallelization
...
59, Complex loop carried dependence of U_new->->,U->-> prevents parallelization
61, Complex loop carried dependence of U_new->->,U->-> prevents parallelization
No, the compiler detected data dependency in the loops and refused to parallelize them. What is the problem?
The __restrict Type Qualifier
Our data arrays (U, Unew, F) are dynamically allocated and are accessed via pointers. To be more precise via pointers to pointers (float **). A pointer is the address of a location in memory. More than one pointer can access the same chunk of memory in the C language, potentially creating data dependency. How can this happen?
Consider a loop:
for (i=1; i<N; i++)
a[i] = b[i] + c[i];
At the first glance there is no data dependency, however the C language puts very few restrictions on pointers. For example arithmetic operations on pointers are allowed. What if b = a - 1? That is b is just a offset by one array index.
The loop becomes
for (i=1; i<N; i++)
a[i] = a[i-1] + c[i];
It is now apparent that the loop has a READ after WRITE dependency and is not vectorizable.
The compiler’s job in deciding on the presence of data dependencies is pretty complex. For simple loops like the one above, modern compilers can automatically detect the potential data dependencies and take care of them. However, if a loop is more complex with more manipulations in indexing, compilers will not try to make a deeper analysis and refuse to vectorize the loop.
Fortunately, you can fix this problem by giving the compiler a hint that it is safe to make optimizations. To assure the compiler that the pointers are safe, you can use the __restrict type qualifier. Applying the __restrict qualifier to a pointer ensures that the pointer is the only way to access the underlying object. It eliminates the potential for pointer aliasing, enabling better optimization by the compiler.
Let’s modify definitions of the arrays (U, Unew, F) applying the __restrict qualifier and recompile the code:
float ** __restrict U;
float ** __restrict Unew;
float ** __restrict F;
nvc laplace2d.c -O3 -acc -ta=tesla -Minfo=accel
Now the loops are parallelized:
50, Loop is parallelizable
Generating implicit copyin(U[:2048][:2048],F[1:2046][1:2046]) [if not already present]
Generating implicit copy(error) [if not already present]
Generating implicit copyout(U_new[1:2046][1:2046]) [if not already present]
52, Loop is parallelizable
Generating Tesla code
50, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
Generating implicit reduction(max:error)
52, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */
57, Generating implicit copyin(U_new[1:2046][1:2046]) [if not already present]
Generating implicit copyout(U[1:2046][1:2046]) [if not already present]
60, Loop is parallelizable
62, Loop is parallelizable
Generating Tesla code
60, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
62, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */
The loops are parallelized and Tesla code is generated! The performance is somewhat better but still slower than serial.
What else may be the problem?
The problem is that the data is copied to the GPU every time the program enters the kernels region and copies the data back to the CPU each time it exits the kernels region. The transfer of data from CPU to GPU is much slower than transfers from the main memory to CPU or from video memory to GPU, so it becomes a huge bottleneck. We don’t need to transfer data at every loop iteration. We could transfer data once at the beginning of the calculations and get it out at the end. OpenACC has a directive to tell the compiler when data needs to be transferred.
The acc data Construct
The acc data construct has five clauses:
- copy
- copyin
- copyout
- create
- present
Their names describe their obvious functions.
- The copy, clause copies data to the accelerator when entering the data region and back from the accelerator to the host when exiting the data region.
- The copyin clause copies data to the accelerator when entering the data region but it does not copy data back
- The copyout is used only to return data from a directive region to the host.
We need to transfer U, Unew and F to the accelerator, but we need only U back. Therefore, we will use copyin and copyout clauses. As we use pointers, compiler does not know dimensions of the arrays, so we need to specify dimensions.
#pragma acc data copyin(U[0:m][0:n], U_new[0:m][0:n], F[0:m][0:n]) copyout(U[0:m][0:n])
Now the code runs much faster!
The acc parallel Construct
- Defines the region of the program that should be compiled for parallel execution on the accelerator device.
- The parallel loop directive is an assertion by the programmer that it is both safe and desirable to parallelize the affected loop.
- The parallel loop construct allows for much more control of how the compiler will attempt to structure work on the accelerator. The loop directive gives the compiler additional information about the next loop in the source code through several clauses
- independent – all iterations of the loop are independent
- collapse(N) - turn the next N loops into one, flattened loop
- tile(N,[M]) break the next 1 or more loops into tiles based on the provided dimensions.
An important difference between the acc kernels and acc parallel constructs is that with kernels the compiler will analyze the code and only parallelize when it is certain that it is safe to do so.
In some cases, the compiler may not be able to determine whether a loop is safe the parallelize, even if you can clearly see that the loop is safely parallel. The kernels construct gives the compiler maximum freedom to parallelize and optimize the code for the target accelerator. It also relies most heavily on the compiler’s ability to automatically parallelize the code.
Fine Tuning Parallel Constructs: the gang, worker, and vector Clauses
OpenACC has 3 levels of parallelism:
- Vector threads work in SIMD parallelism
- Workers compute a vector
- Gangs have 1 or more workers. A gang have shared resources (cahce, streaming multiprocessor ). Gangs work independently of each other.
gang, worker, and vector can be added to a loop clause. Since different loops in a kernels region may be parallelized differently, fine-tuning is done as a parameter to the gang, worker, and vector clauses.
Portability from GPUs to CPUs
We can add OpenMP directives along with the OpenACC directives. Then depending on what options are passed to the compiler we can build ether multiprocessor or accelerator versions.
Let’s apply OpenMP directives and
#pragma omp parallel for private(i) reduction(max:error)
to the loop at line 50 and
#pragma omp parallel for private(i)
to the loop at line 59
nvc laplace2d.c -mp -O3
View NVIDIA HPC-SDK documentation.
Key Points
OpenACC offers a quick path to accelerated computing with less programming effort