Introduction to GPU Programming with OpenACC

Overview

Teaching: 35 min
Exercises: 5 min

Questions

How to program GPU with OpenACC?

Objectives

Learn about programming GPU with openACC

Examples of OpenACC accelerated applications:

VASP 6 (ab initio atomic scale modeling).NVIDIA GPU Accelerated VASP 6 uses OpenACC to Deliver 15X More Performance
TINKER 9 (molecular dynamics)

OpenACC Compilers

GCC
PGI
Nvidia HPC SDK

Solving the Discrete Poisson’s Equation Using Jacobi’s Method.

Poisson’s equation arises in heat flow, diffusion, electrostatic and gravitational potential, fluid dynamics, .. etc. The governing equations of these processes are partial differential equations, which describe how each of the variables changes as a function of all the others.

\[\nabla^2U(x,y)=f(x,y)\]

Here $ \nabla $ is the discrete Laplace operator, $ f(x,y) $ is a known function, and $ U(x,y) $ is the function to be determined.

This equation describes, for example, steady-state temperature of a uniform square plate. To make a solution defined we need to specify boundary conditions, i.e the value of $ U $ on the boundary of our square plate.

We will consider the simple case with the boundaries kept at temperature $ U = 0 $.
We will place a continuous point heat source in the middle of the plate ($ f(x,y)=0 $ everywhere except one hot spot in the middle of the plate.).

Jacobi’s Stencil in 2D.

Common useful iterative algorithm.
For discretization on a uniform spatial grid $ n\times m $ the solution can be found by iteratively computing next value at the grid point $ i,j $ as an average of its four neighboring values and the function $ f(i,j) $.

\[U(i,j,m+1) = ( U(i-1,j,m) + U(i+1,j,m) + U(i,j-1,m) + U(i,j+1,m) + f(i,j) )/4\]

Solution

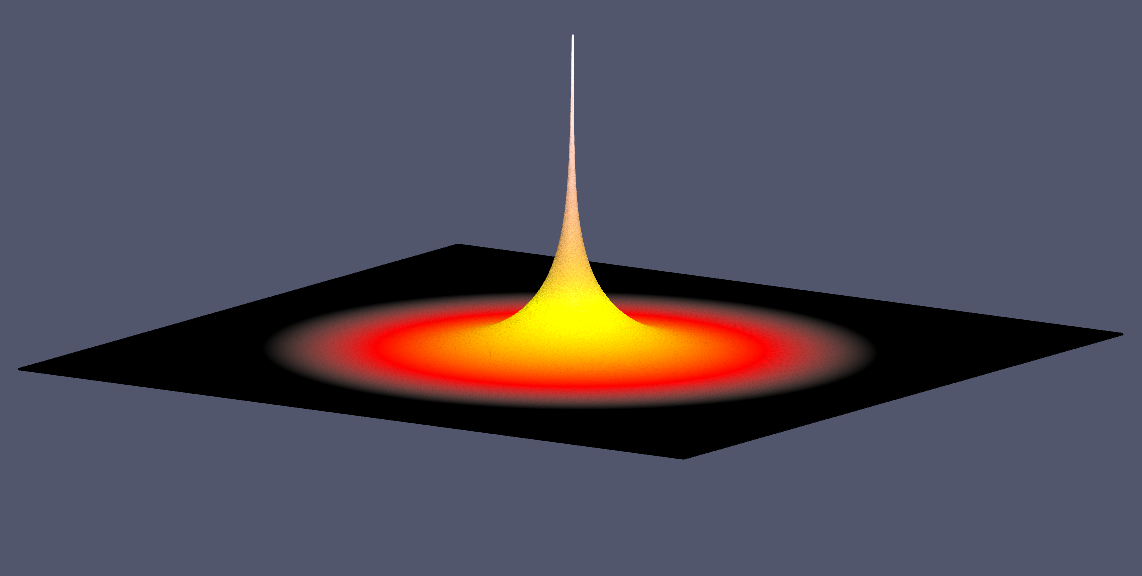
Serial Jacobi Relaxation Code

/* File: laplace2d.c */
#include <math.h>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main(int argc, char **argv)
{
    FILE *output_unit;
    int i, j;
    int n = 1024;
    int m = 1024;            /* Size of the mesh */
    int qn = (int)n * 0.5;   /* x-coordinate of the point heat source */
    int qm = (int)m * 0.5;   /* y-coordinate of the point heat source */
    float h = 0.05;          /* Instantaneous heat */
    int iter_max = 1e8;      /* Maximum number of iterations */
    const float tol = 1e-6f; /* Tolerance */

    struct timespec ts_start, ts_end;
    float time_total;
    float ** U, **U_new;
    float ** F;

    /* Allocate memory */
    F = (float **)malloc(m * sizeof(float *)); /* Heat source array */
    for (i = 0; i < m; i++)
        F[i] = malloc(n * sizeof(float));
    F[qn][qm] = h;                             /* Set point heat source */
    U = (float **)malloc(m * sizeof(float *)); /* Plate temperature */
    for (i = 0; i < m; i++)
        U[i] = malloc(n * sizeof(float));
    U_new = (float **)malloc(m * sizeof(float *)); /* Temporary new temperature */
    for (i = 0; i < m; i++)
        U_new[i] = malloc(n * sizeof(float));

    printf("Jacobi relaxation calculation: %d x %d mesh\n", n, m);
    /* Get calculation  start time */
    clock_gettime(CLOCK_MONOTONIC, &ts_start);

    /* The main loop */
    int iter = 0;       /* Iterration counter */
    float error = 1.0f; /* The initial error */
    while (error > tol && iter < iter_max)
    {
        error = 0.f;
        /* Compute the new temperature  at the point i,j as a weighted average of */
        /* the four neighbors and the heat source function F(i,j) */
        {
            for (j = 1; j < n - 1; j++)
            {
                for (i = 1; i < m - 1; i++)
                {
                    U_new[j][i] = 0.25f * (U[j][i + 1] + U[j][i - 1] + U[j - 1][i] + U[j + 1][i]) + F[j][i];
                    error = fmaxf(error, fabsf(U_new[j][i] - U[j][i]));
                }
            }
            /*  Update temperature */
            for (int j = 1; j < n - 1; j++)
            {
                for (i = 1; i < m - 1; i++)
                    U[j][i] = U_new[j][i];
            }
            if (iter % 200 == 0) /* Print error every 200 iterrations */
                printf("%5d, %0.6e\n", iter, error);
            iter++;
        }
    }

    /* Get end time */
    clock_gettime(CLOCK_MONOTONIC, &ts_end);
    time_total = (ts_end.tv_sec - ts_start.tv_sec) * 1e9 + (ts_end.tv_nsec - ts_start.tv_nsec);
    printf("\nTotal relaxation time is %f sec\n", time_total / 1e9);

    /* Write data to a binary file for paraview visualization */
    char *output_filename = "poisson_1024x1024_float32.raw";
    output_unit = fopen(output_filename, "wb");
    for (j = 0; j < n; j++)
        fwrite(U[j], m * sizeof(float), 1, output_unit);
    fclose(output_unit);
}

Performance of the Serial Code

Compile and run

gcc laplace2d_template.c -lm -O3

The serial code with 2048x2048 mesh does 10,000 iterations in 233 sec. Are the for loops at lines 50, 52, 59, and 61 vectorized?

gcc laplace2d.c -lm -O3 -fopt-info-vec-missed

Performance of the Auto-vectorized Code

Try Intel compiler:

module load intel/2022.1.0
icc -qopt-report=1 -qopt-report-phase=vec -O3 laplace2d.c

Only the for loop at line 52 is vectorized, the code runs in 136 sec.

Parallelizing Jacobi Relaxation Code with OpenACC

The acc kernels Construct

Let’s add a single, simple OpenACC directive before the block containing for loop nests at lines 50 and 59.

#pragma acc kernels

This pragma tells the compiler to generate parallel accelerator kernels (CUDA kernels in our case) for the block of loop nests following the directive.

Compiling with Nvidia HPC SDK

Load the Nvidia HPC module:

module load StdEnv/2020 nvhpc/20.7 cuda/11.0

To compile the code with OpenACC we need to add a couple of options:

tell the nvc compiler to compile OpenACC directives (-acc)
compile for target architecture NvidiaG Tesla GPU (-ta=tesla)

nvc laplace2d.c -O3 -acc -ta=tesla 

Let’s run the program. Uh oh, that’s a bit of a slow-down compared even to our serial CPU code.

Were the loops parallelized?

enable printing information about the parallelization ( add the option -Minfo=accel) and recompile

nvc laplace2d.c -O3 -acc -ta=tesla -Minfo=accel

     50, Complex loop carried dependence of U->->,F->->,U_new->-> prevents parallelization
     52, Complex loop carried dependence of U->->,F->->,U_new->-> prevents parallelization
     ...
     59, Complex loop carried dependence of U_new->->,U->-> prevents parallelization
     61, Complex loop carried dependence of U_new->->,U->-> prevents parallelization

No, the compiler detected data dependency in the loops and refused to parallelize them. What is the problem?

The __restrict Type Qualifier

Our data arrays (U, Unew, F) are dynamically allocated and are accessed via pointers. To be more precise via pointers to pointers (float **). A pointer is the address of a location in memory. More than one pointer can access the same chunk of memory in the C language, potentially creating data dependency. How can this happen?

Consider a loop:

    for (i=1; i<N; i++)
          a[i] = b[i] + c[i];

At the first glance there is no data dependency, however the C language puts very few restrictions on pointers. For example arithmetic operations on pointers are allowed. What if b = a - 1? That is b is just a offset by one array index.

The loop becomes

    for (i=1; i<N; i++)
          a[i] = a[i-1] + c[i];

It is now apparent that the loop has a READ after WRITE dependency and is not vectorizable.

The compiler’s job in deciding on the presence of data dependencies is pretty complex. For simple loops like the one above, modern compilers can automatically detect the potential data dependencies and take care of them. However, if a loop is more complex with more manipulations in indexing, compilers will not try to make a deeper analysis and refuse to vectorize the loop.

Fortunately, you can fix this problem by giving the compiler a hint that it is safe to make optimizations. To assure the compiler that the pointers are safe, you can use the __restrict type qualifier. Applying the __restrict qualifier to a pointer ensures that the pointer is the only way to access the underlying object. It eliminates the potential for pointer aliasing, enabling better optimization by the compiler.

Let’s modify definitions of the arrays (U, Unew, F) applying the __restrict qualifier and recompile the code:

float ** __restrict U;
float ** __restrict Unew;
float ** __restrict F;

nvc laplace2d.c -O3 -acc -ta=tesla -Minfo=accel

Now the loops are parallelized:

     50, Loop is parallelizable
         Generating implicit copyin(U[:2048][:2048],F[1:2046][1:2046]) [if not already present]
         Generating implicit copy(error) [if not already present]
         Generating implicit copyout(U_new[1:2046][1:2046]) [if not already present]
     52, Loop is parallelizable
         Generating Tesla code
         50, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
             Generating implicit reduction(max:error)
         52, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */
     57, Generating implicit copyin(U_new[1:2046][1:2046]) [if not already present]
         Generating implicit copyout(U[1:2046][1:2046]) [if not already present]
     60, Loop is parallelizable
     62, Loop is parallelizable
         Generating Tesla code
         60, #pragma acc loop gang, vector(4) /* blockIdx.y threadIdx.y */
         62, #pragma acc loop gang, vector(32) /* blockIdx.x threadIdx.x */

The loops are parallelized and Tesla code is generated! The performance is somewhat better but still slower than serial.

What else may be the problem?

The problem is that the data is copied to the GPU every time the program enters the kernels region and copies the data back to the CPU each time it exits the kernels region. The transfer of data from CPU to GPU is much slower than transfers from the main memory to CPU or from video memory to GPU, so it becomes a huge bottleneck. We don’t need to transfer data at every loop iteration. We could transfer data once at the beginning of the calculations and get it out at the end. OpenACC has a directive to tell the compiler when data needs to be transferred.

The acc data Construct

The acc data construct has five clauses:

copy
copyin
copyout
create
present

Their names describe their obvious functions.

The copy, clause copies data to the accelerator when entering the data region and back from the accelerator to the host when exiting the data region.
The copyin clause copies data to the accelerator when entering the data region but it does not copy data back
The copyout is used only to return data from a directive region to the host.

We need to transfer U, Unew and F to the accelerator, but we need only U back. Therefore, we will use copyin and copyout clauses. As we use pointers, compiler does not know dimensions of the arrays, so we need to specify dimensions.

#pragma acc data copyin(U[0:m][0:n], U_new[0:m][0:n], F[0:m][0:n]) copyout(U[0:m][0:n])

Now the code runs much faster!

The acc parallel Construct

Defines the region of the program that should be compiled for parallel execution on the accelerator device.
The parallel loop directive is an assertion by the programmer that it is both safe and desirable to parallelize the affected loop.
The parallel loop construct allows for much more control of how the compiler will attempt to structure work on the accelerator. The loop directive gives the compiler additional information about the next loop in the source code through several clauses
- independent – all iterations of the loop are independent
- collapse(N) - turn the next N loops into one, flattened loop
- tile(N,[M]) break the next 1 or more loops into tiles based on the provided dimensions.

An important difference between the acc kernels and acc parallel constructs is that with kernels the compiler will analyze the code and only parallelize when it is certain that it is safe to do so.

In some cases, the compiler may not be able to determine whether a loop is safe the parallelize, even if you can clearly see that the loop is safely parallel. The kernels construct gives the compiler maximum freedom to parallelize and optimize the code for the target accelerator. It also relies most heavily on the compiler’s ability to automatically parallelize the code.

Fine Tuning Parallel Constructs: the gang, worker, and vector Clauses

OpenACC has 3 levels of parallelism:

Vector threads work in SIMD parallelism
Workers compute a vector
Gangs have 1 or more workers. A gang have shared resources (cahce, streaming multiprocessor ). Gangs work independently of each other.

gang, worker, and vector can be added to a loop clause. Since different loops in a kernels region may be parallelized differently, fine-tuning is done as a parameter to the gang, worker, and vector clauses.

Portability from GPUs to CPUs

We can add OpenMP directives along with the OpenACC directives. Then depending on what options are passed to the compiler we can build ether multiprocessor or accelerator versions.

Let’s apply OpenMP directives and

#pragma omp parallel for private(i) reduction(max:error)

to the loop at line 50 and

#pragma omp parallel for private(i)

to the loop at line 59

nvc laplace2d.c -mp -O3

View NVIDIA HPC-SDK documentation.

Key Points

OpenACC offers a quick path to accelerated computing with less programming effort

previous episode

ACENET Summer School - Directive-Based Parallel Programming with OpenMP and OpenACC

lesson home