Introduction

Overview

Teaching: 15 min
Exercises: 10 min

Questions

Why use MPI?

What is MPI?

How do I run an MPI program?

Objectives

Use mpirun and srun

Request resources for MPI from Slurm

Why MPI?

MPI allows utilization of more computers to perform a single task than some of the other parallelization methods we outlined in this workshop (e.g. OpenMP, GPGPU, SIMD). It can also be combined with these other methods. As we have seen there are higher level tools (e.g. Dask, Spark etc. ) which also allow distributed computing. These higher level tools can greatly decrease programming time and provide reasonable parallel speed ups at the expense of the ability to easily understand and control the details of coordination and parallelization.

MPI facilitates communication and coordination among multiple separate machines over a network to perform a single computational task. A problem may be broken up into chunks that each separate machine can operate on and provides a way to communicate results of computations between machines as needed to synchronize and coordinate. One can store a single dataset distributed across the memory of many computers, allowing datasets much larger than the memory of any individual machine to remain in memory while it is operated on.

Below is an example of a fluid dynamics problem solved using this distributed approach with MPI.

This is a model of a star that is radially pulsating with convection occurring near the surface in the hydrogen ionization zone (see sharp change in temperature blue -> red). This simulation is of only a small 2D pie slice section of a full star with periodic boundary conditions at left and right edges. The colour scale indicates the temperature of the gas and the vectors show the convective velocity of the gas. The entire computational grid moves in and out with the radial pulsation of the star. While this 2D simulation admittedly doesn’t push the boundaries of scale it is a good demonstration of how a problem can be solved using MPI.

However this simulation of core convection in a massive star on 1536 cubed grid computed on Compute Canada’s Niagara cluster does push the boundaries of scale. Color shows horizontal velocity. The simulation was conducted by the Computational Stellar Astrophysics group led by Prof Falk Herwig at the University of Victoria.

At the end of the workshop once the necessary building blocks have been presented we will write an MPI parallelized version of a 1D thermal diffusion simulation. While this is admittedly a toy problem many of the important aspects of parallelizing a grid based model will be tackled, such as domain decomposition, guardcells, and periodic boundary conditions. These same problems arose in the radial pulsation simulation and were solved in a similar way to how we will address them in our 1D diffusion simulation. It is also very likely that the core convection simulation had to address similar problems.

What is MPI?

MPI is a standard. MPI stands for Message Passing Interface, a

portable message-passing standard designed by a group of researchers from academia and industry to function on a wide variety of parallel computing architectures. The standard defines the syntax and semantics of a core of library routines useful to a wide range of users writing portable message-passing programs in C, C++, and Fortran. There are several well-tested and efficient implementations of MPI, many of which are open-source or in the public domain.

[Wikipedia]

The Open MPI implementation is available by default on Compute Canada clusters.
MPICH and Intel MPI implementations are also available. Use module spider impi/mpich to see module description and details about how to load those modules.

Running multiple copies of a program

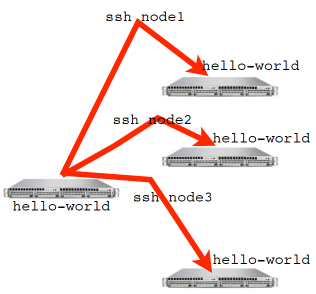
An MPI program, or any program for that matter, can be run with mpirun. mpirun will start N copies of a program. For a mutlinode run mpirun knows the list of nodes your program should run on and ssh’s (or equivalent) to each node and launches the program.

What mpirun does

$ ls

mpi-tutorial  projects  scratch

$ mpirun -np 2 ls

mpi-tutorial  projects  scratch
mpi-tutorial  projects  scratch

$ hostname
$ mpirun -np 4 hostname

Multiple ways to launch an MPI program

In addition there is also the commands mpiexec and srun which can also be used to launch MPI programs. srun is provided by the Slurm scheduler (see slurm srun docs) and provides cluster administrators with better job account than by just running mpirun or mpiexec. Ultimately srun calls down to either mpirun or mpiexec to do the actual launching of the MPI program.

What else does mpirun do?

Assigns an MPI rank to each process
Sets variables that programs written for MPI recognize so that they know which process they are

Number of Processes

Number of processes to use is almost always equal to the number of processors
You can choose different numbers if you want, but think about why you want to!

Interaction with the job scheduler

mpirun behaves a little differently in a job context than outside it. A cluster scheduler allows you to specify how many processes you want, and optionally other information like how many nodes to put those processes on. With Slurm, you can choose the number of process a job has with the option --ntasks <# processes>.

Common slurm options for MPI

The most commonly used slurm options for scheduling MPI jobs are:

--ntasks, specifies the number of process the slurm job has

--nodes, specifies the number of nodes the job is spread across

--ntasks-per-node, specifies the number of tasks or processes per node

Often you use either:

--ntasks if you want to merely specify how many process you want but don’t care how they are arranged with respect to compute nodes,

or

you use the combination of --nodes and --ntasks-per-node to specify how many whole nodes and how many process on each node you want. Typically this would be done if your job can make use of all the cores on one or more nodes. For more details on MPI job scheduling see Compute Canada documentation on MPI jobs.

Try this

What happens if you run the following directly on a login node?
$ mpirun -np 2 hostname
$ mpirun hostname
How do you think mpirun decides on the number of processes if you don’t provide -np?

Now get an interactive shell from the job scheduler and try again:
$ salloc --ntasks=4 --time=2:0:0 
$ mpirun hostname
$ mpirun -np 2 hostname
$ mpirun -np 6 hostname

Key Points

mpirun starts any program

srun does same as mpirun inside a Slurm job

mpirun and srun get task count from Slurm context

MPI Hello World

Overview

Teaching: 15 min
Exercises: 10 min

Questions

What does a basic MPI program look like?

How do I compile an MPI program?

How can I find out about more MPI functions?

Objectives

Compile and run either C or Fortran “Hello MPI World”

Recognize MPI header files and function calls

Know how to find more information about more MPI functions.

Let’s create our first MPI program. If following along with C use the file name hello-world.c or if following along replace the file name extension with .f90. You will also need to add the Fortran code rather than C code to your files.

$ nano hello-world.c

$ nano hello-world.f90

and add the following C/Fortran code.

#include <stdio.h>
#include <mpi.h>

int main(int argc, char **argv) {
  
  int rank, size, ierr;
  
  ierr=MPI_Init(&argc,&argv);
  ierr=MPI_Comm_size(MPI_COMM_WORLD, &size);
  ierr=MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  
  printf("Hello, World, from task %d of %d\n",rank, size);
  
  ierr=MPI_Finalize();
  return 0;
}

program helloworld
  use mpi
  implicit none
  integer :: rank, comsize, ierr
  
  call MPI_Init(ierr)
  call MPI_Comm_size(MPI_COMM_WORLD, comsize, ierr)
  call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierr)
  
  print *,'Hello World, from task ', rank, 'of', comsize
  
  call MPI_Finalize(ierr)
end program helloworld

Notice the MPI function calls and constants (beginning with MPI_) in the following C and Fortran sample codes. Let save and exit nano.

Compiling

MPI is a Library for Message-Passing. MPI is not built into the compiler. It is a library that can be linked in while building the final executable as you would link in any other library. It is available for the C,C++ and Fortran languages. There are even ways to use MPI with python and R (see mpi4py and Rmpi ).

However, there are compiler wrappers (mpicc, mpic++, mpif90, mpif77) which automatically include the needed options to compile and link MPI programs.

Once the MPI program is compiled they can be launched using the mpirun command.

As previously mentioned, the easiest way to compile an MPI program is to use one of the compiler wrappers. For our C code we use the mpicc compiler wrapper. For our Fortran code we use the mpif90 compiler wrapper. These compiler wrappers add various -I, -L, and -l options as appropriate for MPI. Including the --showme option shows which underlying compiler and options are being used by the compiler wrapper.

$ mpicc --showme hello-world.c -o hello-world

gcc hello-world.c -o hello-world
  -I/cvmfs/soft.computecanada.ca/easybuild/software/2017/avx2/Compiler/gcc7.3/openmpi/3.1.4/include
  -L/cvmfs/soft.computecanada.ca/easybuild/software/2017/avx2/Compiler/gcc7.3/openmpi/3.1.4/lib
  -lmpi

So mpicc runs gcc hello.world.c -o hello-world with a number of options (-I, -L, -l) to make sure the right libraries and headers are available for compiling MPI programs. Let’s take a look at this again for mpif90 compiler.

Finally let’s do the actual compilation with

$ mpicc hello-world.c -o hello-world

$ mpif90 hello-world.f90 -o hello-world

And then run it with two processes.

$ mpirun -np 2 hello-world

Hello, World, from task 0 of 2
Hello, World, from task 1 of 2

MPI Library reference

So far we have seen the following MPI library functions:

Each of the above functions listed above are a link to a page about them on OpenMPI docs. On these pages you can get information about what functions do and what the expected parameters for them are along with any errors they might return.

If you go to the main page of OpenMPI docs you can see that there are many MPI library functions (>200). However, there are not nearly so many concepts. In this workshop we will cover only a handful of these functions but with these few functions we can accomplish some pretty powerful things.

Varying the number of processors

Try different numbers of processes with the -np option.

Solution

$ mpirun -np 2 hello-world

Hello, World, from task 1 of 2
Hello, World, from task 0 of 2

$ mpirun -np 4 hello-world

Hello, World, from task 0 of 4
Hello, World, from task 2 of 4
Hello, World, from task 3 of 4
Hello, World, from task 1 of 4

$ mpirun -np 8 hello-world

--------------------------------------------------------------------------
There are not enough slots available in the system to satisfy the 8 slots
that were requested by the application:
  hello-world

Either request fewer slots for your application, or make more slots available
for use.
--------------------------------------------------------------------------

As might be expected, each core generates its own line output. If however, you try to run with more processes than cores available you will get the above message and the program will not run.

Running multiple times

Try running the program multiple times with the same number of processes
Solution
$ mpirun -np 4 hello-world
Hello, World, from task 0 of 4
Hello, World, from task 1 of 4
Hello, World, from task 2 of 4
Hello, World, from task 3 of 4
$ mpirun -np 4 hello-world
Hello, World, from task 1 of 4
Hello, World, from task 2 of 4
Hello, World, from task 3 of 4
Hello, World, from task 0 of 4
Notice that the order the messages are printed out does not remain the same from run to run. This is because different processes are not all executing the lines of a program in lockstep with each other. You should be careful not to write your program to depend on the order in which processes execute statements relative to each other as it is not dependable.

Key Points

C requires #include <mpi.h> and is compiled with mpicc

Fortran requires use mpi and is compiled with mpif90

commands mpicc, mpif90 and others are wrappers around compilers

Hello World in detail

Overview

Teaching: 10 min
Exercises: 0 min

Questions

What order are MPI programs executed?

What do the MPI functions in hello-world do?

What is a communicator?

Objectives

Understand the MPI “boilerplate” code

Know what a race condition is and how it might arise

Know what an MPI communicator is

Let’s start to explore the MPI functions in our hello-world program in detail. However before we do that let’s first talk a little bit more about how MPI programs are executed to help better frame our discussion of these MPI functions.

Program flow in MPI

Each process running an MPI program executes the same program in order from start to finish as a serial program would. The difference is there are multiple copies of the same program running simultaneously on different processes. At a given time during execution, different processes are very likely executing different lines of code. From one run of the MPI code to another the order in which processes reach a given line of code may change. In other words there is no reason that node 2 will execute statement 1 before node 1, as is illustrated below. This order of execution can change from run to run.

If you program happens to depend on this order of execution this can lead to something called a race condition in which results or the stability of the program can depend on which process gets to which line of code first. Dependencies of this sort can usually be avoided by using some sort of synchronization mechanism (e.g. a blocking MPI function such as MPI_Barrier, MPI_Send, etc. ) and/or careful program design.

At first glance this seems like running a program this way won’t get us anything as we are just replicating the work. However, we can write the program in such a way that different process will work on different parts of the data and even perform different tasks. Let’s start looking at the MPI functions in our hello-world program in a little more detail to see how.

Back to Hello-world

Let’s have a look at the C and Fortran hello-world programs again and talk about the MPI functions and constants.

#include <stdio.h>
#include <mpi.h>

int main(int argc, char **argv) {
  
  int rank, size, ierr;
  
  ierr=MPI_Init(&argc,&argv);
  ierr=MPI_Comm_size(MPI_COMM_WORLD, &size);
  ierr=MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  
  printf("Hello, World, from task %d of %d\n",rank, size);
  
  ierr=MPI_Finalize();
  return 0;
}

program helloworld
  use mpi
  implicit none
  integer :: rank, comsize, ierr
  
  call MPI_Init(ierr)
  call MPI_Comm_size(MPI_COMM_WORLD, comsize, ierr)
  call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierr)
  
  print *,'Hello World, from task ', rank, 'of', comsize
  
  call MPI_Finalize(ierr)
end program helloworld

Code (C/Fortran)	Description
`#include <mpi.h>` `use mpi`	Imports declarations for MPI functions and constants in the same way C and Fortran import other header files and modules.
`MPI_Init(&argc,&argv)` `call MPI_INIT(ierr)`	Initialize MPI. Must come first. Returns error code in ierr, if any.
`MPI_Comm_size(MPI_COMM_WORLD, &size)` `call MPI_Comm_size(MPI_COMM_WORLD, comsize, ierr)`	Stores the number of process in `size`/`comsize`.
`MPI_Comm_rank(MPI_COMM_WORLD, &rank)` `call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierr)`	Stores the current process number in `rank`.
`MPI_Finalize()` `call MPI_FINALIZE(ierr)`	Finish and clean up MPI. Must come last. Returns error code in ierr.

C / Fortran differences

The C version ‘MPI_Init’ passes in the program’s argument count and argument value array, while the Fortran version does not. From the OpenMPI docs page for MPI_Init it says

Open MPI accepts the C/C++ argc and argv arguments to main, but neither modifies, interprets, nor distributes them

The fortran versions of the MPI functions pass the error code back in the ierr parameter, while C versions of the MPI functions return the error code. For example in C int ierr=MPI_Init(&argc,&argv);, here ierr would contain the error code.

Now that each process has a unique ID or rank and we know the total number of processes, size/comsize, we might start to guess at how we could use this to divide up our work. Perhaps something like this:

#define ARRAY_SIZE 1000

...

int array[ARRAY_SIZE];
int workSize=ARRAY_SIZE/size;
int workStart=workSize*rank;

for(int i=workStart;i<workStart+workSize;++i){
  
  //do something with array[i]
  
}

...

At this point we can already start to image how we can do some useful work with MPI. However, this simple example doesn’t do much beyond what something like GNU Parallel could do for us with a serial program. MPI’s functionality really starts to show when we start talking about message passing. However, before we dive into message passing let’s talk about the MPI_COMM_WORLD constant and communicators in generall a little bit.

Communicators

The MPI_COMM_WORLD is a constant which identifies the default MPI communicator. So what’s a communicator? A communicator is a collection of process and a mapping between an ID or rank and those processes. All process are a member of the default MPI communicator MPI_COMM_WORLD. There can be multiple communicators in an MPI program and process can have different ranks within different communicators. In addition not all processes have to be in all communicators. Communicators are used when passing messages between process to help coordinate and organize which processes should get which messages.

The function MPI_Comm_size(MPI_COMM_WORLD,&size) gets the size of, or number of processes in, the communicator passed as an argument (in this case MPI_COMM_WORLD). The function MPI_Comm_rank(MPI_COMM_WORLD,&rank) gets the ID or rank of the current process within that communicator (in this case MPI_COMM_WORLD). Ranks within the communicator range for 0 to size-1 where size is the size of the communicator.

It is possible to create your own communicators with MPI_Comm_create, however for the rest of this workshop we will only use the default MPI_COMM_WORLD communicator.

Writting to stdout

Beware! Standard does not require that every process can write to stdout! However, in practice this is often possible, though not always desirable because the output can get jumbled and out of order, even within single print statements.

Key Points

MPI processes have rank from 0 to size-1

MPI_COMM_WORLD is the ordered set of all processes

Functions MPI_Init, MPI_Finalize, MPI_Comm_size, MPI_Comm_rank are fundamental to any MPI program

Send and receive

Overview

Teaching: 15 min
Exercises: 10 min

Questions

What is point-to-point communication?

What is collective communication?

How to pass a point-to-point message?

Objectives

Write code to pass a message from one process to another

MPI is a Library for Message-Passing

Message passing in MPI is what allows it to solve large non-separable problems on distributed hardware. If communication between processes is not required for your problem do not use MPI, use something like GNU Parallel.

Communication and coordination between processes is done by sending and receiving messages. Each message involves a function call from at least two processes running the program. One process that has the data and one process that needs the data. It maybe that more than one process needs data only stored on one process or one process needs data scattered across multiple processes this type of communication involving many process are called collective communication.

Three basic sets of functionality provided by MPI:

Pairwise (or point-to-point) communications via messages (e.g. MPI_Ssend, MPI_Recv)
Collective synchronization and communication (e.g. MPI_Barrier, MPI_Scatter, MPI_Gather, MPI_Reduce, MPI_Allreduce)
Efficient routines for getting data from memory into messages and vice versa (e.g. MPI_Pack, MPI_Unpack)

Our “Hello World” program doesn’t actually pass any messages. Let’s fix this by adding some pairwise communication, but first we need to know a little more about messages.

Pairwise Messages

Pairwise messages have a sender and a receiver process. Each message has a unique non-negative integer tag to identify a particular message to ensure sending and receiving calls are for the correct message if there are multiple messages being sent between two processes.

messages

An MPI message consists of count elements of type MPI_TYPE which are contiguous in memory beginning at sendptr. MPI types map to existing types in the language for example characters, integers, floating point numbers. A list of available MPI constants (both data type constants and other constants) can be found on this MPICH documentation page.

To send a message the sender must call an MPI function to send the message. For the message to be received the receiver must call an MPI function to receive the message. Below are the pairs of C and Fortran functions to send and receive a message. Given our example diagram above src_rank=0, dest_rank=3, MPI_TYPE=MPI_CHAR. Return argument status contains information about the message, for example the process rank that sent the message.

MPI_Status status;
ierr=MPI_Ssend(sendptr, count, MPI_TYPE, dest_rank, tag, Communicator);
ierr=MPI_Recv(rcvptr, count, MPI_TYPE, src_rank, tag,Communicator, status);

integer status(MPI_STATUS_SIZE)
call MPI_SSEND(sendarr, count, MPI_TYPE, dest_rank,tag, Communicator, ierr)
call MPI_RECV(rcvarr, count, MPI_TYPE, src_rank, tag,Communicator, status, ierr)

Our first message

Now that we have a basic understanding of how to send messages let’s try it out.

$ cp hello-world.c firstmessage.c
$ nano firstmessage.c

Remember to replace .c with .f90 if working with Fortran code.

#include <stdio.h>
#include <mpi.h>

int main(int argc, char **argv){
  
  int rank, size, ierr;
  int sendto, recvfrom;       /* tasks to send to and receive from */
  int tag=1;                  /* shared tag to label msgs */
  char sendmessage[]="Hello"; /* text to send */
  char getmessage[6];         /* place to receive */
  MPI_Status rstatus;         /* MPI_Recv status info */
  
  ierr=MPI_Init(&argc,&argv);
  ierr=MPI_Comm_size(MPI_COMM_WORLD, &size);
  ierr=MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  
  int count=6;
  if(rank==0){
    sendto=1;
    ierr=MPI_Ssend(sendmessage, count, MPI_CHAR, sendto, tag,
                   MPI_COMM_WORLD);
    printf("%d: Sent message <%s>\n",rank, sendmessage);
  }
  else if(rank==1){
    recvfrom=0;
    ierr=MPI_Recv(getmessage, count, MPI_CHAR, recvfrom, tag,
                  MPI_COMM_WORLD, &rstatus);
    printf("%d: Got message  <%s>\n",rank, getmessage);
  }
  
  ierr=MPI_Finalize();
  return 0;
}

NOTE MPI_CHAR is used in C to map to the C char datatype, while MPI_CHARACTER is used in Fortran to map to Fortran character datatype.

program firstmessage
  
  use mpi
  implicit none
  integer :: rank, comsize, ierr
  integer :: sendto, recvfrom  ! task to send,recv from 
  integer :: ourtag=1          ! shared tag to label msgs
  character(5) :: sendmessage  ! text to send
  character(5) :: getmessage   ! text to recieve 
  integer, dimension(MPI_STATUS_SIZE) :: rstatus
  integer :: count=5
  
  call MPI_Init(ierr)
  call MPI_Comm_size(MPI_COMM_WORLD, comsize, ierr)
  call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierr)
  
  if(rank==0) then
    sendmessage='hello'
    sendto=1;
    call MPI_Ssend(sendmessage, count, MPI_CHARACTER, sendto, ourtag,
      MPI_COMM_WORLD,ierr) 
    print *,rank, 'sent message <',sendmessage,'>'
  else if(rank==1) then
    recvfrom=0;
    call MPI_Recv(getmessage, count, MPI_CHARACTER, recvfrom, ourtag,
      MPI_COMM_WORLD, rstatus,ierr)
    print *,rank, 'got message  <',getmessage,'>'
  endif
  
  call MPI_Finalize(ierr)
end program firstmessage

Now let’s compile our program with either

$ mpicc -o firstmessage firstmessage.c

$ mpif90 -o firstmessage firstmessage.f90

depending on C or Fortran. Now let’s run it with two processes

$ mpirun -np 2 ./firstmessage

0: Sent message <Hello>
1: Got message <Hello>

Key Points

Functions MPI_Ssend, MPI_Recv

Types MPI_CHAR, MPI_Status

More than two processes

Overview

Teaching: 20 min
Exercises: 15 min

Questions

How do we manage communication among many processes?

Objectives

Write code to pass messages along a chain

Write code to pass messages around a ring

MPI programs routinely work with thousands of processors. In our first message we used ifs to write an MPI_Ssend and an MPI_Recv for each process. Applying this idea niavely to large numbers of processes would lead to something like:

if(rank==0){...}
if(rank==1){...}
if(rank==2){...}
...

which gets a little tedious somewhere at or before rank=397. More typically programs calculate the ranks they need to communicate with. Let’s imagine processors in a line. How could we calculate the left and right neighbour ranks?

One way to calculate our neighbour’s ranks cloud be left=rank-1, and right=rank+1. Let’s think for a moment what would happen if we wanted to send a message to the right. Each process would have an MPI_Ssend call to send to their right neighbour and each process would also have an MPI_Recv call to receive a message from their left neighbour. But what will happen at the ends? It turns out that there are special constants that can be used as sources and destinations of messages. If MPI_PROC_NULL is used the send or receive is skipped.

MPI_ANY_SOURCE

MPI_ANY_SOURCE is similar to MPI_PROC_NULL but can only be used when receiving a message. It will allow a receive call to accept a message sent from any process.

Let’s try out sending a set of messages to the processes on the right.

$ cp firstmessage.c secondmessage.c

Remember to replace .c with .f90 if working with Fortran code.

#include <stdio.h>
#include <mpi.h>

int main(int argc, char **argv) {
  
  int rank, size, ierr;
  int left, right;
  int tag=1;
  double msgsent, msgrcvd;
  MPI_Status rstatus;
  
  ierr=MPI_Init(&argc, &argv);
  ierr=MPI_Comm_size(MPI_COMM_WORLD, &size);
  ierr=MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  
  left=rank-1;
  if(left<0){
    left=MPI_PROC_NULL;
  }
  
  right=rank+1;
  if(right>=size){
    right=MPI_PROC_NULL;
  }
  
  msgsent=rank*rank;
  msgrcvd=-999.;
  int count=1;
  ierr=MPI_Ssend(&msgsent, count, MPI_DOUBLE, right,tag,
                 MPI_COMM_WORLD); 
  
  ierr=MPI_Recv(&msgrcvd, count, MPI_DOUBLE, left, tag, MPI_COMM_WORLD,
                &rstatus);
  
  printf("%d: Sent %lf and got %lf\n", rank, msgsent, msgrcvd);
  
  ierr=MPI_Finalize();
  return 0;
}

NOTE MPI_DOUBLE is used in C to map to the C double datatype, while MPI_DOUBLE_PRECISION is used in Fortran to map to Fortran double precision datatype.

program secondmessage
use mpi
implicit none

  integer :: ierr, rank, comsize
  integer :: left, right
  integer :: tag
  integer :: status(MPI_STATUS_SIZE)
  double precision :: msgsent, msgrcvd

  call MPI_INIT(ierr)
  call MPI_COMM_RANK(MPI_COMM_WORLD,rank,ierr)
  call MPI_COMM_SIZE(MPI_COMM_WORLD,comsize,ierr)

  left = rank-1
  if (left < 0) left = MPI_PROC_NULL 
  right = rank+1
  if (right >= comsize) right = MPI_PROC_NULL 

  msgsent = rank*rank
  msgrcvd = -999.
  tag = 1

  call MPI_Ssend(msgsent, 1, MPI_DOUBLE_PRECISION, right, &
                 tag, MPI_COMM_WORLD, ierr)
            
  call MPI_Recv(msgrcvd, 1, MPI_DOUBLE_PRECISION, left, & 
                tag, MPI_COMM_WORLD, status, ierr)
                
  print *, rank, 'Sent ', msgsent, 'and recvd ', msgrcvd

  call MPI_FINALIZE(ierr)

end program secondmessage

Now let’s compile our program with either

$ mpicc -o secondmessage secondmessage.c

$ mpif90 -o secondmessage secondmessage.f90

and run with

$ mpirun -np 4 ./secondmessage

Sent 0.000000 and got -999.000000
Sent 1.000000 and got 0.000000
Sent 4.000000 and got 1.000000
Sent 9.000000 and got 4.000000

Periodic boundaries

In many problems it is helpful to wrap data around at the boundaries of the grid being modelled. For example later in our 1D diffusion exercise, we will use periodic boundary conditions which allows heat flow out of one end of our thin wire to enter the other end making our thin wire a ring. This sort of periodic boundary condition often works well in physical simulations.

Let’s try having our messages wrap around from our right most process to our left most process. Periodic Send Right

Add periodic message passing
$ cp secondmessage.c thirdmessage.c
$ nano thirdmessage.c
Remember to replace .c with .f90 if working with Fortran code. And modify the code so that left is either size-1 for C or comsize-1 for Fortran when at the inner most edge and so that right is 0 at the outer most edge.

Then compile and run.

Hint: you may need to press ctrl+c after running the program.
Solution
  . . .
  left=rank-1;
  if(left<0){
    left=size-1;
  }
  
  right=rank+1;
  if(right>=size){
    right=0;
  }
  . . .
  . . .
  left = rank-1
  if (left < 0) left = comsize-1
  right = rank+1
  if (right >= comsize) right = 0
  . . .
Then compile with either
$ mpicc -o thirdmessage thirdmessage.c
or
$ mpif90 -o thirdmessage thirdmessage.f90
and run with
$ mpirun -np 4 ./thirdmessage
The program hangs and must be killed by pressing ctrl+c. This is because the MPI_Ssend call blocks until a matching MPI_Recv has been initiated.

Key Points

A typical MPI process calculates which other processes it will communicate with.

If there is a closed loop of procs sending to one another, there is a risk of deadlock.

All sends and receives must be paired, at time of sending.

Types MPI_DOUBLE (C), MPI_DOUBLE_PRECISION (Ftn)

Constants MPI_PROC_NULL, MPI_ANY_SOURCE

Blocking and buffering

Overview

Teaching: 10 min
Exercises: 15 min

Questions

Is there an easier way to manage multiple processes?

Objectives

Describe variants on MPI_Ssend

Describe buffering and blocking

Use MPI_SendRecv

Why did we get a deadlock with periodic boundaries but not when we didn’t? To help answer that question let’s take a look at the messaging passing process in a little more detail.

Different ways to send messages

What happens when a message is sent between processes? The data stored in memory of one process must be copied to the memory of the other process. This coping is not instantaneous especially since the two processes are very likely not starting to send and receive the message at exactly the same time. So how is this copying of memory between processes coordinated?

There are two main ways the copying of memory between processes can be coordinated:

Synchronous: the sending and receiving process must coordinate their sending and receiving so that no buffering of data is needed and a minimal amount of copying of data occurs.
Buffered: a buffer is used to store the data to be sent until the matching receive call happens.

In addition to synchronous or buffered methods of sending data there is also the question of when the send, or even the receive, function should return. Should they return as quickly as possible or should the return once the messages sending has been completed? This leads to the idea of blocking, if the send or receive function waits until the matching send or receive call has reached some point in its execution before returning this is known as a blocking send or receive. In the case of buffered sends the blocking/non-blocking nature refers waiting until data is coped into the buffer and not that the message has been received. For more details on the topics of synchronous, buffered, and blocking point-to-point MPI messages see MPI: The Complete Reference.

Buffering requires data to be copied into and out of a buffer which means more memory will be used and it will take more processor time to copy the data into a buffer as compared to a synchronous send. However, using a buffer means that you can modify the original data as soon as it has been copied into the buffer. Synchronous sends however, require that the original data being sent is not modified until the data has been sent.

Using non-blocking sends and receives allows one to overlap computations with communication, however DO NOT modify the send buffer or read from the receive buffer until the messages have completed. To know if a message has completed check with MPI_Wait or MPI_Test. To allow the greatest flexibility to optimize the message passing for particular use cases a number of send and receive functions have been defined which incorporate different combinations of Synchronous, Buffered, and Blocking/Non-blocking messaging.

Let’s have a look at some of the available send and receive functions.

Sends

MPI_Send: blocking, buffering or synchronous send. Buffering or synchronous depend on size of message and MPI library implementor’s choice.
MPI_Ssend: blocking, synchronous send with no buffering.
MPI_Bsend: blocking, buffered send. It will block until the data is copied to the buffer. You are responsible for supplying the buffer with MPI_Buffer_attach and knowing how big it has to be. WARNING: it is bigger than just the data you want to send.
MPI_Isend : non-blocking, maybe buffered or synchronous. All non-blocking functions require MPI_Wait or MPI_Test to test when a message completes so that send data can be modified or freed.
MPI_Rsend: ready send, meaning a matching receive call must have already been posted at the time the send has been initiated. You are responsible for ensuring this; it is an error if this is not the case.
MPI_Issend: non-blocking, synchronous send.
MPI_Ibsend: non-blocking, buffered send.
MPI_Irsend: non-blocking, ready send.

Recvs

MPI_Recv: blocking receive.
MPI_Irecv: non-blocking receive.

Wow there are a lot of different sends. Luckily after this we are going to keep it pretty simple. No buffering or checking for messages to complete will happen in this workshop.

Why did we deadlock?

Let’s examine what happened before we added the periodic boundaries. In this case processor 3 was sending to MPI_PROC_NULL while processor 0 was receiving from MPI_RPOC_NULL. We used MPI_Ssend which is a blocking send. This means that the function will block program execution until at least some part of the matching MPI_Recv call has been initiated. This means that all processes end up waiting at the MPI_Ssend function for the matching MPI_Recv to begin. Luckily process 3 was sending to MPI_PROC_NULL and so skips the send and proceeds to the MPI_Recv. After this each process can proceed in turn after the call to the matching MPI_Recv has initiated.

Results of secondmessage

With this in mind, what would happen when we don’t have any processes sending to MPI_PROC_NULL? All process will be waiting in the MPI_Ssend functions for the matching MPI_Recv function to be called. However, if they are all waiting in the MPI_Ssend no processes will be able to call an MPI_Recv function as those happen afterwards. This is why our periodic send deadlocked. So how would we fix this?

How to avoid deadlock?

One way we could avoid the deadlock only using the MPI functions we have already used is to split up the message passing into two sets of messages where we pair send and receives.

even ranks send, odd ranks receive
odd ranks send, even ranks receive

Another way we could solve this issue is by using the non-blocking sends, however, we would then need to later check for the completeness of the message to continue.

There is another MPI function which is very useful for situations like this MPI_Sendrecv. This is a blocking call combining both a send and receive. However the send and receive within that call will not block each other, only that the entire function will block. The send and receive buffers must be different and may not overlap. The source and destination processes do not have to be the same nor do the data type, tag or size of the messages. The send and receive components of this call could be handling two totally unrelated messages, except for perhaps the time at which the both the sending and receiving of those messages occur.

This is typical of MPI; with the very basics you can do almost anything, even if you have to jump through some hoops - but there are often more advanced routines which can help do things more easily and faster.

`MPI_Sendrecv` = Send + Recv

C syntax

send recieve

FORTRAN syntax

send reciev

Use `MPI_Sendrecv` to solve deadlock

$ cp thirdmessage.c fourthmessage.c
$ nano fourthmessage.c

Remember to replace .c with .f90 if working with Fortran code.

Solution

  . . .
  msgsent=rank*rank;
  msgrcvd=-999.;
  int count=1;
  ierr=MPI_Sendrecv(&msgsent, count, MPI_DOUBLE, right, tag,
                    &msgrcvd, count, MPI_DOUBLE, left,  tag,
                    MPI_COMM_WORLD, &rstatus);
  
  printf("%d: Sent %lf and got %lf\n", rank, msgsent, msgrcvd);
  . . .

  . . .
  msgsent= rank*rank
  msgrcvd= -999.
  tag=1
  
  call MPI_Sendrecv(msgsent, 1, MPI_DOUBLE_PRECISION, right, tag, &
                    msgrcvd, 1, MPI_DOUBLE_PRECISION, left,  tag, &
                    MPI_COMM_WORLD, status, ierr)
  
  print *, rank, 'Sent ', msgsent, 'and recvd ', msgrcvd
  . . . 

Then compile with either

$ mpicc -o fourthmessage fourthmessage.c

$ mpif90 -o fourthmessage fourthmessage.f90

and run with

$ mpirun -np 4 ./fourthmessage

Sent 0.000000 and got 9.000000
Sent 1.000000 and got 0.000000
Sent 9.000000 and got 4.000000
Sent 4.000000 and got 1.000000

Key Points

There are advanced MPI routines that solve most common problems. Don’t reinvent the wheel.

Function MPI_SendRecv

Collective communication

Overview

Teaching: 15 min
Exercises: 10 min

Questions

What is the best way to do global sums and the like in MPI?

Objectives

Write code to global minimum, mean (from sum), and maximum with basic functions

Do the same with higher-level functions and compare

So far we have been working with point-to-point communication and with that you can construct most of the communication and with blocking send/receive communication even synchronization to some degree, though I wouldn’t recommend doing synchronization that way. However, when the communication involves all the processes there are communication patterns for which MPI has supplied specialized communication functions to manage the details for you. This is much like when we used the combined MPI_Sendrecev function to combine the sending and receiving. MPI handled all the coordination for us to avoid deadlock.

Min, mean, max

Consider a common task of calculating the min/mean/max of a bunch of numbers (in this case random) in the range $-1$..$1$. The min/mean/max should tend towards $-1$,$0$,$+1$ for large $N$.

Serial

Let’s take a quick look at the serial code for a min/mean/max calculation and think about how we might parallelize it.

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char **argv) {
  
  /* generate random data */
  const int nx=1500;
  float *dat = (float *)malloc(nx * sizeof(float));
  srand(0);
  int i;
  for(i=0;i<nx;i++){
    dat[i] = 2*((float)rand()/RAND_MAX)-1.;
  }
  
  /* find min/mean/max */
  float datamin = 1e+19;
  float datamax =-1e+19;
  float datamean = 0;
  for(i=0;i<nx;i++){
    
    if(dat[i]<datamin){
      
      datamin=dat[i];
    }
    if(dat[i]>datamax){
      
      datamax=dat[i];
    }
    datamean += dat[i];
  }
  datamean /= nx;
  
  free(dat);
  
  printf("Min/mean/max = %f,%f,%f\n", datamin,datamean,datamax);
  
  return 0;
}

program randomdata
  
  implicit none
  integer ,parameter :: nx=1500
  real,allocatable :: dat(:)
  
  integer :: i,n
  real :: datamin,datamax,datamean

  ! generate random data
  allocate(dat(nx))
  call random_seed(size=n)
  call random_seed(put=[(i,i=1,n)])
  call random_number(dat)
  dat=2*dat-1.
  
  ! find min/mean/max
  datamin= minval(dat)
  datamax= maxval(dat)
  datamean= (1.*sum(dat))/nx
  
  deallocate(dat)
  
  print *,'min/mean/max =', datamin, datamean, datamax
  
  return
end

Parallel

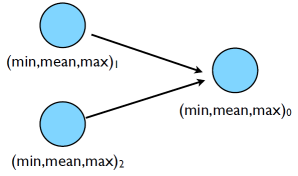
How do we parallelize it with MPI? Let’s have each process generated a portion of $N$ and then have them compute local min/mean/max, send the local result to some process, say process $0$ to compute the final result and report it back to us. Graphically this would look something like:

min mean max

Complete the code

Below are partial programs in both C and Fortran to implement the algorithm we just described. Choose one, copy it to a file called minmeanmax-mpi.c or minmeanmax-mpi.f90, and fill in the missing function parameters for both the MPI_Ssend and MPI_Recv calls identified by the **** S T U F F G O E S H E R E **** comments. Compile and run it.

#include <stdio.h>
#include <mpi.h>
#include <stdlib.h>

int main(int argc, char **argv) {
  
  const int nx=1500;
  float *dat;
  int i;
  float datamin, datamax, datamean;
  float minmeanmax[3];
  float globminmeanmax[3];
  int ierr;
  int rank, size;
  int tag=1;
  int masterproc=0;
  MPI_Status status;
  
  ierr = MPI_Init(&argc, &argv);
  ierr = MPI_Comm_size(MPI_COMM_WORLD,&size);
  ierr = MPI_Comm_rank(MPI_COMM_WORLD,&rank);
  
  /* generate random data */
  dat = (float *)malloc(nx * sizeof(float));
  srand(rank);
  for (i=0;i<nx;i++){
    
    dat[i] = 2*((float)rand()/RAND_MAX)-1.;
  }
  
  /* find min/mean/max */
  datamin = 1e+19;
  datamax =-1e+19;
  datamean = 0;
  for (i=0;i<nx;i++) {
    
    if (dat[i] < datamin) datamin=dat[i];
    if (dat[i] > datamax) datamax=dat[i];
    datamean += dat[i];
  }
  datamean /= nx;
  free(dat);
  minmeanmax[0] = datamin;
  minmeanmax[2] = datamax;
  minmeanmax[1] = datamean;
  
  printf("Proc %d min/mean/max = %f,%f,%f\n",
         rank, minmeanmax[0],minmeanmax[1],minmeanmax[2]);
  if (rank != masterproc) {
    
    ierr = MPI_Ssend( /***** S T U F F   G O E S   H E R E *****/ );
  }
  else {
      globminmeanmax[0] = datamin;
      globminmeanmax[2] = datamax;
      globminmeanmax[1] = datamean;
      for (i=1;i<size;i++) {
        
        ierr = MPI_Recv( /***** S T U F F   G O E S   H E R E *****/ );
        
        globminmeanmax[1] += minmeanmax[1];
        
        if (minmeanmax[0] < globminmeanmax[0]){
          
          globminmeanmax[0] = minmeanmax[0];
        }
        
        if (minmeanmax[2] > globminmeanmax[2]){
          
          globminmeanmax[2] = minmeanmax[2];
        }
      }
      globminmeanmax[1] /= size;
      printf("Min/mean/max = %f,%f,%f\n", globminmeanmax[0],
             globminmeanmax[1],globminmeanmax[2]);
  }
  
  ierr = MPI_Finalize();
  
  return 0;
}

program randomdata
  use mpi
  implicit none
  integer,parameter :: nx=1500
  real, allocatable :: dat(:)
  
  integer :: i,n
  real    :: datamin, datamax, datamean
  real    :: globmin, globmax, globmean
  integer :: ierr, rank, comsize
  integer :: ourtag=5
  real, dimension(3) :: sendbuffer, recvbuffer
  integer, dimension(MPI_STATUS_SIZE) :: status
  
  call MPI_INIT(ierr)
  call MPI_COMM_SIZE(MPI_COMM_WORLD, comsize, ierr)
  call MPI_COMM_RANK(MPI_COMM_WORLD, rank, ierr)
  
  ! random data
  allocate(dat(nx))
  call random_seed(size=n)
  call random_seed(put=[(rank,i=1,n)])
  call random_number(dat)
  dat = 2*dat - 1.
  
  ! find min/mean/max
  datamin = minval(dat)
  datamax = maxval(dat)
  datamean= (1.*sum(dat))/nx
  deallocate(dat)
  
  if (rank /= 0) then
    sendbuffer(1) = datamin
    sendbuffer(2) = datamean
    sendbuffer(3) = datamax
    
    call MPI_SSEND()  ! ***** S T U F F   G O E S   H E R E *****
    
  else
    globmin = datamin
    globmax = datamax
    globmean = datamean
    do i=2,comsize
      
      call MPI_RECV() ! ***** S T U F F   G O E S   H E R E *****
      
      if (recvbuffer(1) < globmin) globmin=recvbuffer(1)
      if (recvbuffer(3) > globmax) globmax=recvbuffer(3)
      globmean = globmean + recvbuffer(2)
    enddo
    globmean = globmean / comsize
  endif
  
  print *,rank, ': min/mean/max = ', datamin, datamean, datamax
  
  if (rank==0) then
    print *, 'global min/mean/max = ', globmin, globmean, globmax
  endif
  
  call MPI_FINALIZE(ierr)
end

Are the sends and receives adequately paired?

Solutions

 . . .
 if(rank!=masterproc){
   
   ierr=MPI_Ssend(minmeanmax,3,MPI_FLOAT,masterproc,tag,MPI_COMM_WORLD);
 } 
 else{
   
   globminmeanmax[0]=datamin;
   globminmeanmax[2]=datamax;
   globminmeanmax[1]=datamean;
 }
 for (i=1;i<size;i++) {
   
   ierr = MPI_Recv(minmeanmax,3,MPI_FLOAT,MPI_ANY_SOURCE,tag,
                   MPI_COMM_WORLD,&status);
   
   globminmeanmax[1] += minmeanmax[1];
   
   if(minmeanmax[0] < globminmeanmax[0]){
     
     globminmeanmax[0] = minmeanmax[0];
   }
   
   if(minmeanmax[2] > globminmeanmax[2]){
     
     globminmeanmax[2] = minmeanmax[2];
   }
 }
 globminmeanmax[1] /= size;
 printf("Min/mean/max = %f,%f,%f\n", globminmeanmax[0],globminmeanmax[1],
        globminmeanmax[2]);
 . . .

 . . .
 datamin = minval(dat)
 datamax = maxval(dat)
 datamean = (1.*sum(dat))/nx
 deallocate(dat)  
 
 if (rank /= 0) then
   sendbuffer(1) = datamin
   sendbuffer(2) = datamean
   sendbuffer(3) = datamax
   call MPI_Ssend(sendbuffer, 3, MPI_REAL, 0, ourtag, MPI_COMM_WORLD, ierr)  
 else
   globmin = datamin
   globmax = datamax
   globmean = datamean
   
   do i=2,comsize 
     call MPI_Recv(recvbuffer, 3, MPI_REAL, MPI_ANY_SOURCE, &
                   ourtag, MPI_COMM_WORLD, status, ierr)
     if (recvbuffer(1) < globmin) globmin=recvbuffer(1)
     if (recvbuffer(3) > globmax) globmax=recvbuffer(3)
     globmean = globmean + recvbuffer(2)
   enddo
   
   globmean = globmean / comsize
 endif

 print *,rank, ': min/mean/max = ', datamin, datamean, datamax
 . . .

Then compile with

$ mpicc -o minmeanmax-mpi minmeanmax-mpi.c

$ mpif90 -o minmeanmax-mpi minmeanmax-mpi.f90

and run

$ mpirun -np 4 ./minmeanmax-mpi

Proc 0 min/mean/max = -0.999906,0.001355,0.999987
Min/mean/max = -0.999906,0.009106,0.999987
Proc 1 min/mean/max = -0.999906,0.001355,0.999987
Proc 2 min/mean/max = -0.998753,0.038589,0.998893
Proc 3 min/mean/max = -0.997360,-0.004877,0.999729

A better method

This works, but we can do better, or rather there is an MPI function which can do better. This method requires $(P-1)$ messages where $P$ is the number of processes. In addition if all processes need the result it will be $2(P-1)$. A better method would be:

Processes are paired up
One process sends their local results to the other
The other process receiving the result computes the sub results
Repeat steps 1-3 pairing up only processes which received and computed sub results in step 3 until only one process remains.

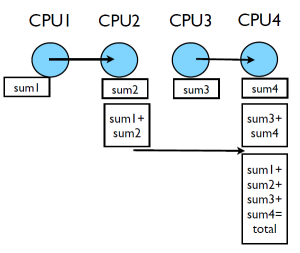
bettersumming

The cases illustrated here have fairly small numbers of processes, the reduction in number of messages sent is fairly minimal. However, if we scale up so the number of processes, $P$, is very large this method can start to show considerable improvements. The maximum number messages sent is $log2(P)$. The same method can be used to send the total back to all processes. There for the total time for communication $T_{comm}$ can be related to the number of processes $P$ and the time for communicating a single message, $C_{comm}$ as

[T_{comm}=2\log_2(P)C_{comm}]

This process of combining many numbers into a single result is referred to as a reduction process. This algorithm will work for a variety of operators ($+$,$\times$,$min()$,$max()$, …).

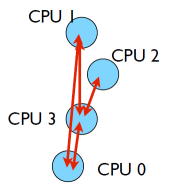
Collective operations

MPI supplies some functions which will perform the above process for us, MPI_Reduce if only one process needs the result, and MPI_Allreduce if all processes need the result.

collective operation

As an example an MPI_Reduce function call might look this:

  call MPI_REDUCE(datamin, globmin, 1, MPI_REAL, MPI_MIN, &
                  0, MPI_COMM_WORLD, ierr)

As opposed to the pairwise messages we’ve seen so far, all processes in the communicator must participate and they may not proceed until all have participated in the function call. While you can implement these patterns yourself with Sends/Recvs, it will likely be less clear and slower, especially for large numbers of processes.

Run the AllReduce code

Copy the below code C or Fortran into minmeanmax-allreduce.c or minmeanmax-allreduce.f90}

#include <stdio.h>
#include <mpi.h>
#include <stdlib.h>

int main(int argc, char **argv) {
  
  const int nx=1500;  // number of data per process
  float *dat;         // local data
  int i;
  float datamin, datamax, datasum, datamean;
  float globmin, globmax, globsum, globmean;
  int ierr;
  int rank, size;
  MPI_Status status;

  ierr = MPI_Init(&argc, &argv);
  ierr = MPI_Comm_size(MPI_COMM_WORLD,&size);
  ierr = MPI_Comm_rank(MPI_COMM_WORLD,&rank);

  /*generate random data at each process*/
  dat = (float *)malloc(nx * sizeof(float));
  srand(rank);
  for (i=0;i<nx;i++) {
    dat[i] = 2*((float)rand()/RAND_MAX)-1.;
  }

  /*find local min/sum/max*/
  datamin = 1e+19;
  datamax =-1e+19;
  datasum = 0;

  for (i=0;i<nx;i++) {
    if (dat[i] < datamin) datamin=dat[i];
    if (dat[i] > datamax) datamax=dat[i];
    datasum += dat[i];
  }
  datamean = datasum/nx;
  free(dat);

  printf("Proc %d min/mean/max = %f,%f,%f\n",
         rank, datamin, datamean, datamax);

  /* combine local results*/
  ierr = MPI_Allreduce(&datamin, &globmin, 1, MPI_FLOAT, MPI_MIN,
                  MPI_COMM_WORLD);
  
  ierr = MPI_Allreduce(&datasum, &globsum, 1, MPI_FLOAT, MPI_SUM,
                       MPI_COMM_WORLD);
  ierr = MPI_Allreduce(&datamax, &globmax, 1, MPI_FLOAT, MPI_MAX,
                       MPI_COMM_WORLD);
  globmean = globsum/(size*nx);

  /* to just send to task 0:
  ierr = MPI_Reduce(&datamin, &globmin, 1, MPI_FLOAT, MPI_MIN,
                    0, MPI_COMM_WORLD);
   */

  if (rank == 0) {
     printf("Global min/mean/max = %f, %f, %f\n",
             globmin, globmean, globmax);
  }

  ierr = MPI_Finalize();
  return 0;
}

  program randomdata
  use mpi
  implicit none

  integer,parameter :: nx=1500
  real, allocatable :: dat(:)

  integer :: i,n
  real    :: datamin, datamax, datamean
  real    :: globmin, globmax, globmean
  integer :: rank, comsize, ierr

  call MPI_INIT(ierr)
  call MPI_COMM_RANK(MPI_COMM_WORLD,rank,ierr)
  call MPI_COMM_SIZE(MPI_COMM_WORLD,comsize,ierr)

  ! random data
  allocate(dat(nx))
  call random_seed(size=n)
  call random_seed(put=[(rank,i=1,n)])
  call random_number(dat)
  dat = 2*dat - 1.

  ! find local min/mean/max
  datamin = minval(dat)
  datamax = maxval(dat)
  datamean= (1.*sum(dat))/nx
  deallocate(dat)

  print *,rank,': min/mean/max = ', datamin, datamean, datamax

  ! combine data
  call MPI_ALLREDUCE(datamin, globmin, 1, MPI_REAL, MPI_MIN, &
                    MPI_COMM_WORLD, ierr)

  ! to just send to task 0:
  !  call MPI_REDUCE(datamin, globmin, 1, MPI_REAL, MPI_MIN,
  !&                    0, MPI_COMM_WORLD, ierr)

  call MPI_ALLREDUCE(datamax, globmax, 1, MPI_REAL, MPI_MAX, &
                   MPI_COMM_WORLD, ierr)
  call MPI_ALLREDUCE(datamean, globmean, 1, MPI_REAL, MPI_SUM, &
                   MPI_COMM_WORLD, ierr)
  globmean = globmean/comsize
  if (rank == 0) then
     print *, rank,': Global min/mean/max=',globmin,globmean,globmax
  endif

  call MPI_FINALIZE(ierr)
  end program randomdata

Examine it, compile it, test it.

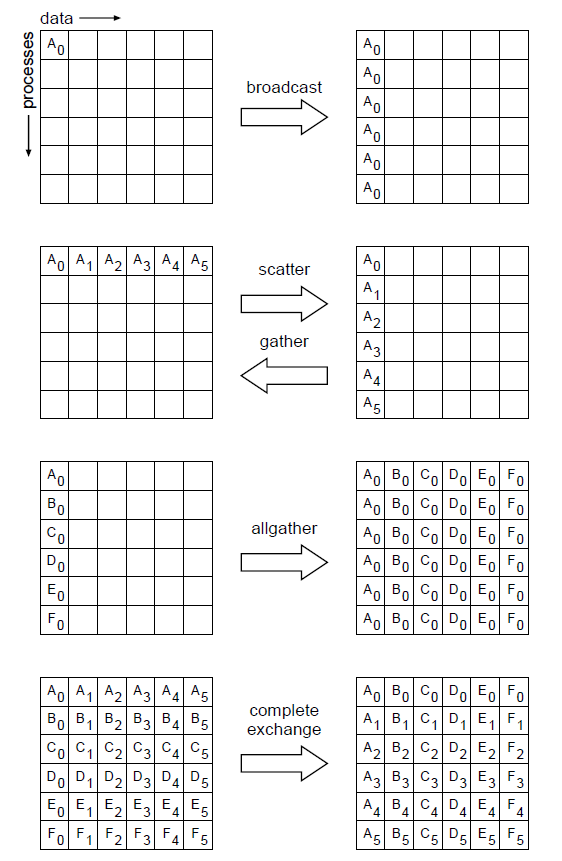
Common patterns of communication

Here are some families of MPI routines that implement common communication patterns.

MPI_Bcast: Broadcast data from one process to all— every process gets a copy
MPI_Scatter: Scatter data from one process to all— every process gets a different slice
MPI_Gather: Collect data from all processes to one process, opposite of Scatter
MPI_AllGather: A variation on Gather where the result is then distributed to all processes
MPI_AllToAll: Scatter/Gather from all procs to all procs— In other words, a complete exchange (of some data structure)
MPI_Allreduce: Global reduction (e.g. sum, max, min, …) where the result is then broadcast to all procs
MPI_Barrier: Forces all processes to synchronize, i.e. wait for the last one to catch up before moving on

By “families” we mean that there are several related routines in each family, e.g. MPI_Scatter, MPI_IScatter, MPI_ScatterV, MPI_IScatterV

collective patterns

Key Points

Collective operations involve all processes in the communicator.

Functions MPI_Reduce, MPI_AllReduce

Types MPI_FLOAT (C), MPI_REAL (Ftn)

Constants MPI_MIN, MPI_MAX, MPI_SUM

Diffusion simulation

Overview

Teaching: 10 min
Exercises: 30 min

Questions

What is involved in adapting a whole program to MPI?

Objectives

Use a finite-difference simulation to explore MPI parallelization

Diffusion Equation

The change in temperature of the wire over time can be modelled using a 1-dimensional partial differential equation, the thermal diffusion equation:

[\frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2}]

where $T$ is temperature, $t$ is time, $x$ is position, $D$ is the “diffusion coefficient”.

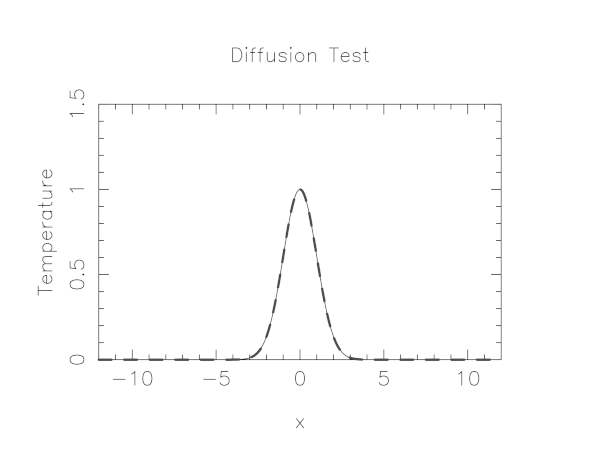
1D diffusion - serial result

To use a partial differential equation to model with a computer how a quantity, in this case the temperature along a wire changes over time, we must discretize that quantity onto a finite set of grid points. The more grid points, the more closely it approximates a real continuous wire. At each of these grid points we can then set some initial temperature and from that use our thermal diffusion equation to calculate a temperature after some time passes, the time step. We can repeat this process moving from the last state to the next new state in order to calculate how the temperature along the wire changes over time.

Discretizing Derivatives

How can we translate our continuous thermal diffusion equation to our discretization temperature grid that we can use to model this physical problem with a computer. Lets start by looking at the partial derivative of temperature with respect to position on the right hand of the equation.

[\frac{\partial^2 T}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial T}{\partial x}]

Breaking it down even further, lets focus at first just on the first order partial derivative of temperature with respect to position. We can approximate the partial derivative with finite differences between grid points.

[\frac{\partial T}{\partial x} \approx \frac{\Delta T}{\Delta x}]

1D diffusion - serial result

If we have an equal grid spacing, $\Delta x$, the spacing between successive grid points will be constant along our grid. If we then label each $T$ along our discretization of the wire with an $i$ to indicate at which grid point it is located, we can write our partial derivative like this

[\frac{\Delta T}{\Delta x}\biggr

{i+1/2} = \frac{ T{i+1}-T_{i} }{ \Delta x }]

That is, the partial derivative of $T$ with respect to position at the mid point ($i+1/2$) between grid cells $i$ and $i+1$. We can this use this to approximate our second order partial differential of temperature with respect to position in the same way

[\frac{\partial^2 T}{\partial x^2}\biggr

_{i} \approx \frac{\frac{\Delta T}{\Delta x}\biggr

_{i+1/2}-\frac{\Delta T}{\Delta x}\biggr

{i-1/2}}{\Delta x}=\frac{T{i+1}-2T_i+T_{i-1}}{(\Delta x)^2}]

Now lets recall our original equation that we are trying to discretize

[\frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2}]

We now have a representation for the right hand side that we can translate into computer code, however, we still need to deal with the left hand side, the time derivative. We can do exactly the same procedure we did for the spatial derivative. Lets define $n$ to represent a particular point in time (like $i$ represented a particular point in space). We can also approximate the partial differential with respect to time by differences in temperature from one time to the next. Doing so we get

[\frac{T^{n+1}{i}-T^{n}_i}{\Delta t} \approx D \frac{T{i+1}^n-2T_i^n+T_{i-1}^n}{(\Delta x)^2}]

Note that I have replaced the second order partial diffiental with respect to position with our finite difference representation. Isolating for the new temperature we get

[T^{n+1}{i} \approx T^{n}_i + \frac{D \Delta t}{(\Delta x)^2}(T{i+1}^n-2T_i^n+T_{i-1}^n)]

This approximation will allow us to compute a new temperature $T$ given the previous temperatures. This approximation uses three grid points to approximate our second order partial differential. The number and relative position of the surrounding points used in computing a quantity in a given cell is often referred to as a “stencile”.

diffusion equation

Build & run serial version

In mpi-tutorial/diffusion is a serial code which simulates the heat flow in a thin wire where the initial condition is that the wire has a very hot spot in the center and the surrounding portions of the wire are cooler. Using the thermal diffusion equation with the discretized version we outline above this code simulates the diffusion of heat from the hot spot to the cooler parts of the wire.

The code uses a simple graphics library called pgplot to draw the temperature profile. You’ll need to have X11 running in your SSH client in order to see the plot. In either case, it will emit many timesteps and error estimates to standard output.

$ git clone https://github.com/acenet-arc/mpi-tutorial.git
$ cd mpi-tutorial/diffusion
$ git pull origin master   # get latest code updates
$ module load pgplot
$ make diffusionc    # or make diffusionf 
$ ./diffusionc       # or ./diffusionf

Step = 0, Time = 5.77154e-05, Error = 3.04144e-07
Step = 1, Time = 0.000115431, Error = 3.74087e-07
.
.
.
Step = 99998, Time = 5.76987, Error = 0.00566646
Step = 99999, Time = 5.76993, Error = 0.00566676

If The following module(s) are unknown: "pgplot"

Load the following module before attempting to load the pgplot module
$ module load arch/avx2
$ module load pgplot

Domain Decomposition

To solve this in parallel, each process must be responsible for some segment of space, i.e. a chunk of the wire.

A very common approach to parallelizing on distributed memory computers
Maintain Locality; need local data mostly, this means only surface data needs to be sent between processes.
Pictures of a few problems being solved with domain decomposition:

domain decomposition

Implement a diffusion equation in MPI

Given our update equation for the temperature:

[T^{n+1}{i} \approx T^{n}_i + \frac{D \Delta t}{(\Delta x)^2}(T{i+1}^n-2T_i^n+T_{i-1}^n)]

we will have the below stencil:

diffusion equation

The question then becomes, what do we do at the edges of the local sub domains on each process, since to compute the new temperature, $T_{i}^{n+1}$, will will need information about temperatures at the previous timestep $n$ from other processors local sub domains?

Guardcells

Job 1 needs info on Job 2’s first zone, Job 2 needs info on Job 1’s last zone
Pad array with `guardcells’ and fill them with the info from the appropriate node by messagepassing or shared memory

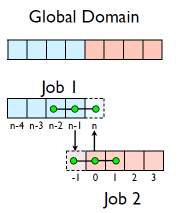
guardcells

Do computation
guardcell exchange: each process has to do 2 sendrecvs
- its rightmost cell with neighbor’s leftmost
- its leftmost cell with neighbor’s rightmost
- Need a convention to avoid deadlock
- Everyone do right-filling first, then left-filling (say)
- What happens at absolute left and absolute right ends of everything? Pick one:
- Periodic boundary conditions, as if the wire were a loop
- Fixed-temperature boundary conditions, temperature in first, last zones some fixed value

Hands-on: MPI diffusion

Convert the serial version of the diffusion program to a parallel version.

$ cp diffusionf.f90 diffusionfmpi.f90

$ cp diffusionc.c diffusionc-mpi.c

Edit with nano to make an MPI version. This will involve the following components:

add standard MPI calls: init, finalize, comm_size, comm_rank
Figure out how many points each process is responsible for (localsize=totpoints/size)
Figure out neighbors, left/right
Compute the new temperature on the local grid
At end of each time step, exchange guardcells; use sendrecv
Get total error

Then build with:

$ make diffusionf-mpi

$ make diffusionc-mpi

Test on 1..8 procs

MPI routines we know so far

MPI_Status status;

ierr = MPI_Init(&argc,&argv);	
ierr = MPI_Comm_size(communicator, &size);
ierr = MPI_Comm_rank(communicator, &rank);
ierr = MPI_Send(sendptr, count, MPI_TYPE, destination, tag, communicator);
ierr = MPI_Recv(recvptr, count, MPI_TYPE, source,      tag, communicator, &status);

ierr = MPI_Sendrecv(sendptr, count, MPI_TYPE, destination, tag,
                    recvptr, count, MPI_TYPE, source,      tag, communicator, &status);

ierr = MPI_Allreduce(&mydata, &globaldata, count, MPI_TYPE, MPI_OP, Communicator);

Communicator -> MPI_COMM_WORLD
MPI_Type -> MPI_FLOAT, MPI_DOUBLE, MPI_INT, MPI_CHAR...
MPI_OP -> MPI_SUM, MPI_MIN, MPI_MAX,...

integer status(MPI_STATUS_SIZE)

call MPI_INIT(ierr)
call MPI_COMM_SIZE(Communicator, size, ierr)
call MPI_COMM_RANK(Communicator, rank, ierr)
call MPI_SSEND(sendarr, count, MPI_TYPE, destination, tag, Communicator, ierr)
call MPI_RECV(recvarr,  count, MPI_TYPE, destination, tag, Communicator, status, ierr)

call MPI_SENDRECV(sendptr, count, MPI_TYPE, destination, tag, &
                  recvptr, count, MPI_TYPE, source,      tag, Communicator, status, ierr)

call MPI_ALLREDUCE(mydata, globaldata, count, MPI_TYPE, MPI_OP, Communicator, ierr)

Communicator -> MPI_COMM_WORLD
MPI_Type -> MPI_REAL, MPI_DOUBLE_PRECISION, MPI_INTEGER, MPI_CHARACTER,...
MPI_OP -> MPI_SUM, MPI_MIN, MPI_MAX,...

Key Points

Finite differences, stencils, guard cells

Where to go next

Overview

Teaching: 5 min
Exercises: 0 min

Questions

Where can I learn more about MPI?

Objectives

References

MPI standards can be found at the MPI Forum. In particular, the MPI 3.1 standard is laid out in this PDF.

The default MPI implementation on Compute Canada clusters is Open MPI. Manual pages can be found at www.open-mpi.org

The default version of Open MPI may differ from one cluster to another, but you can find what version and change it with module commands. See Using modules at the Compute Canada documentation wiki.

There are online tutorials for learning MPI, including these from:

And finally, an anti-reference. Or something. In late 2018 or early 2019 Jonathan Dursi, who created the original version of this workshop, published an essay entitled:

HPC is dying, and MPI is killing it

Its intended audience is people already working in high-performance computing, but has some very cogent things to say about what’s wrong with MPI. Too long; didn’t read? MPI is over 30 years old, and showing its age. Computing is a fast-moving field. If you are lucky enough to be starting a brand-new project that requires massive parallelism, look carefully at newer technologies than MPI.

Key Points

ACENET Summer School - MPI

Introduction

Overview

Why MPI?

What is MPI?

Running multiple copies of a program

Multiple ways to launch an MPI program

What else does mpirun do?

Number of Processes

Interaction with the job scheduler

Common slurm options for MPI

Try this

Key Points

MPI Hello World

Overview

Compiling

MPI Library reference

Varying the number of processors

Solution

Running multiple times

Solution

Key Points

Hello World in detail

Overview

Program flow in MPI

Back to Hello-world

C / Fortran differences

Communicators

Writting to stdout

Key Points

Send and receive

Overview

MPI is a Library for Message-Passing

Pairwise Messages

Our first message

Key Points

More than two processes

Overview

MPI_ANY_SOURCE

Periodic boundaries

Add periodic message passing

Solution

Key Points

Blocking and buffering

Overview

Different ways to send messages

Sends

Recvs

Why did we deadlock?

How to avoid deadlock?

MPI_Sendrecv = Send + Recv

C syntax

FORTRAN syntax

Use MPI_Sendrecv to solve deadlock

Solution

Key Points

Collective communication

Overview

Min, mean, max

Serial

Parallel

Complete the code

Solutions

A better method

Collective operations

Run the AllReduce code

Common patterns of communication

Key Points

Diffusion simulation

Overview

Diffusion Equation

Discretizing Derivatives

Build & run serial version

If The following module(s) are unknown: "pgplot"

Domain Decomposition

Implement a diffusion equation in MPI

Guardcells

Hands-on: MPI diffusion

Key Points

Where to go next

`MPI_ANY_SOURCE`

`MPI_Sendrecv` = Send + Recv

Use `MPI_Sendrecv` to solve deadlock

If `The following module(s) are unknown: "pgplot"`